
由规则三知,实轴上的根轨迹是由0至1线段 和-1至-∞线段。 由规则五的分离点方程可求出根轨迹与实轴 的交点,即由方程 ds(s-1)(s2+2s+2) =0 ds s+1 得a4+23+a2-2=0,解极值方程得到4个 根分别为ou1=0.550=-1.5504=-0.5±j0.75 显然,01和02为根轨迹与实轴交点的合理值,即 01和02为根轨迹的分离点。 11
11 由规则三知,实轴上的根轨迹是由0至1线段 和-1至-∞线段。 由规则五的分离点方程可求出根轨迹与实轴 的交点,即由方程 得 ,解极值方程得到4个 根分别为 , , 显然, 和 为根轨迹与实轴交点的合理值,即 和 为根轨迹的分离点。 0 s 1 s(s 1)(s 2s 2) ds d s 2 = + − + + = 0 3 2 2 4 3 2 + + − = 0.55 1 = 1.55 2 = − 0.5 0.75 3,4 = − j 1 2 1 2

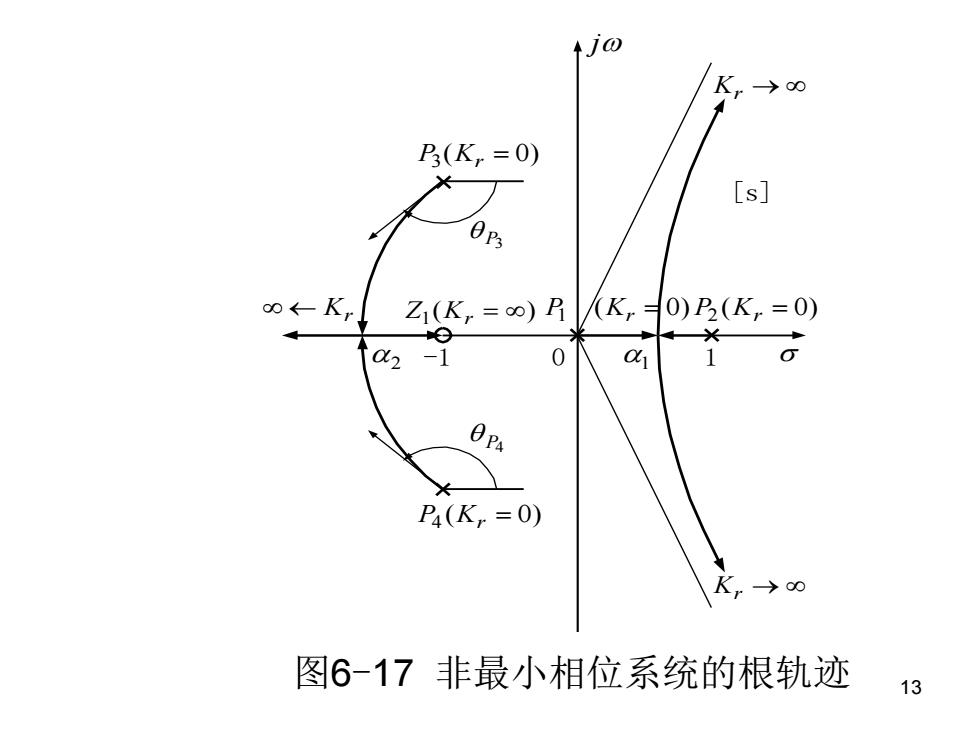
由规则六可求出共轭复数极点p3和p4的起 始角分别为 0p3=F180°+90°-135°-153.4°-90°=-108.6° 6p4=-0p3=108.6° 根轨迹与虚轴无交点。最后绘制出该系统的 根轨迹如图6-17所示。 该非最小相位系统除了有位于S平面右半 部的开环零、极点外,其绘制根轨迹的规则和步 骤与最小相位系统完全相同。需要指出的是,如 果非最小相位系统是正反馈系统,在绘制根轨迹 时应遵循第四节介绍的0°相角条件。 12
12 由规则六可求出共轭复数极点 和 的起 始角分别为 根轨迹与虚轴无交点。最后绘制出该系统的 根轨迹如图6-17所示。 该非最小相位系统除了有位于S平面右半 部的开环零、极点外,其绘制根轨迹的规则和步 骤与最小相位系统完全相同。需要指出的是,如 果非最小相位系统是正反馈系统,在绘制根轨迹 时应遵循第四节介绍的0°相角条件。 p3 4 p = 180 + 90 −135 −153.4 − 90 = −108.6 3p = − =108.6 p4 p3
K,→0 乃(K,=0) [s] 0P3 ←-Kr Z1(K,=o)乃 /K,O)P(K,=0) 02 a OPA P4(K,=0) 图6-17非最小相位系统的根轨迹 13
13 j [s] ( ) Z1 Kr = ( 0) P2 Kr = ( 0) P3 Kr = 2 -1 0 1 Kr → Kr 1 ( 0) P4 Kr = P3 P4 Kr → ( 0) P1 Kr = 图6-17 非最小相位系统的根轨迹

设某负反馈系统的开环传递函数为 G(s)H(s)= K(1-S) (t>0,T>0) s(1+Ts) 系统的特征方程为 1+G(s)H(s)=1+ K(1-S) =1-K(- 1=0 s(1+Ts) s(Ts+1) K(s-1) =1 s(Ts+1) 根轨迹方程与正反馈系统的一样,其幅值条件 和相角条件分别为 K(w-) s(Ts+D ∠(-1)-∠s-∠(Ts+1)=2km
14 设某负反馈系统的开环传递函数为 ( 0, 0) (1 ) (1 ) ( ) ( ) + − = T s Ts K s G s H s 0 ( 1) ( 1) 1 (1 ) (1 ) 1 ( ) ( ) 1 = + − = − + − + = + s Ts K s s Ts K s G s H s 系统的特征方程为 1 ( 1) ( 1) = + − s Ts K s 根轨迹方程与正反馈系统的一样,其幅值条件 和相角条件分别为 1 ( 1) ( 1) = + − s Ts K s (s −1) − s − (Ts +1) = 2k

§6-4系统性能分析 自动控制系统的稳定性,由它的闭环极点 唯一确定,其动态性能与系统的闭环极点和零 点在S平面上的分布有关。因此确定控制系统闭 环极点和零点在S平面上的分布,特别是从已知 的开环零、极点的分布确定闭环零、极点的分 布,是对控制系统进行分析必须首先要解决的 问题。解决的方法之一,是第三章介绍的解析 法,即求出系统特征方程的根。解析法虽然比 较精确,但对四阶以上的高阶系统是很困难的。 15
15 §6-4系统性能分析 自动控制系统的稳定性,由它的闭环极点 唯一确定,其动态性能与系统的闭环极点和零 点在S平面上的分布有关。因此确定控制系统闭 环极点和零点在S平面上的分布,特别是从已知 的开环零、极点的分布确定闭环零、极点的分 布,是对控制系统进行分析必须首先要解决的 问题。解决的方法之一,是第三章介绍的解析 法,即求出系统特征方程的根。解析法虽然比 较精确,但对四阶以上的高阶系统是很困难的