
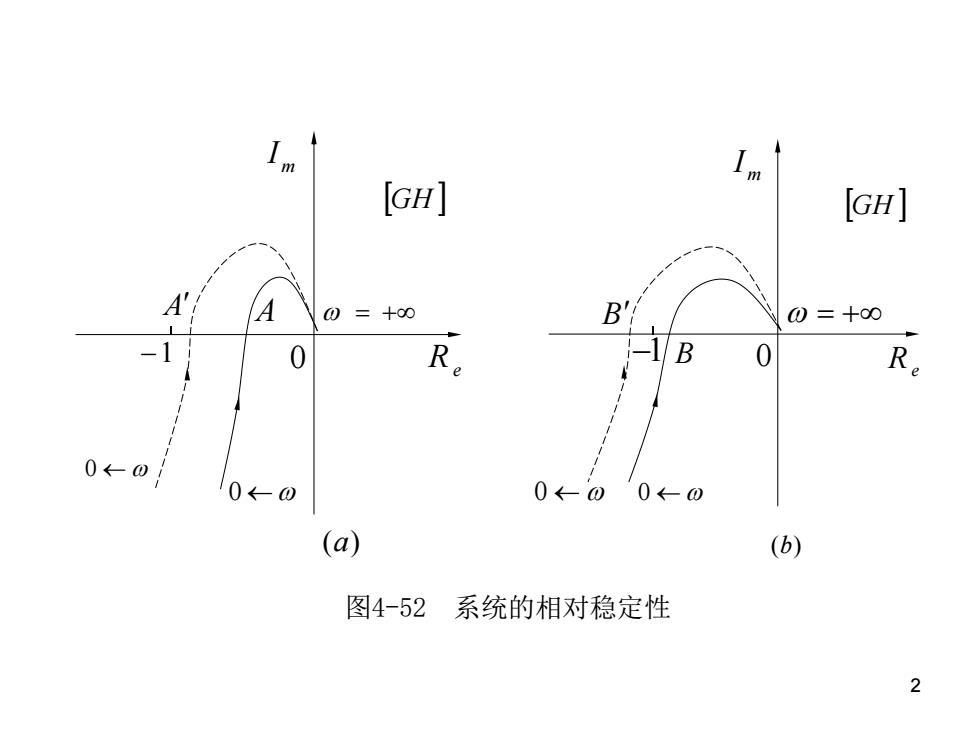
§4-5 控制系统的相对稳定性 一、相对稳定性 在工程应用中,由于环境温度的变化、元件的老化以及元件的更换 等,会引起系统参数的改变,从而有可能破坏系统的稳定性。因此在选 择元件和确定系统参数时,不仅要考虑系统的稳定性,还要求系统有一 定的稳定程度,这就是自动控制系统的相对稳定性问题。 例如,图4-52(a)和(b)所示的两个最小相位系统的开环频率 特性曲线(实线)没有包围(~1,0)点,由奈氏判据知它们都是稳定的系 统,但图4-52(a)所示系统的频率特性曲线与负实轴的交点A距离 (-1,0)点较远,图4-52(b)所示系统的频率特性曲线与负实轴的交 点B距离(-1,0)点较近。假定系统的开环放大系统由于系统参数的改 变比原来增加了百分之五十,则图4-52(a)中的A点移动到A’点,仍在 (-1,j0点右侧,系统还是稳定的;而图4-52(b)中的B点则移到(-1,j0)点 的左侧(B’点),系统便不稳定了。可见,前者较能适应系统参数的 变化,即它的相对稳定性比后者好。 1
1 § 4-5 控制系统的相对稳定性 一、相对稳定性 在工程应用中,由于环境温度的变化、元件的老化以及元件的更换 等,会引起系统参数的改变,从而有可能破坏系统的稳定性。因此在选 择元件和确定系统参数时,不仅要考虑系统的稳定性,还要求系统有一 定的稳定程度,这就是自动控制系统的相对稳定性问题。 例如,图 4-52(a)和(b)所示的两个最小相位系统的开环频率 特性曲线(实线)没有包围 点,由奈氏判据知它们都是稳定的系 统,但图 4-52( a )所示系统的频率特性曲线与负实轴的交点 A 距离 点较远,图 4-52(b)所示系统的频率特性曲线与负实轴的交 点 B 距离 点较近。假定系统的开环放大系统由于系统参数的改 变比原来增加了百分之五十,则图4-52(a)中的A点移动到A’点,仍在 点右侧,系统还是稳定的;而图4-52(b)中的B点则移到 点 的左侧(B’点),系统便不稳定了。 可见,前者较能适应系统参数的 变化,即它的相对稳定性比后者好。 (1, j0) (1, j0) (1, j0) (1, j0) (1, j0)
[GH] [GH] 0=+00 B' 0=+0∞ Re 0 Re 0←-0 0←-0 0←00←-⊙ (a) (b) 图4-52系统的相对稳定性 2
2 m I 0 0 0 GH Re (a) 1 A A m I 0 0 0 GH Re B1 B (b) 图4-52 系统的相对稳定性
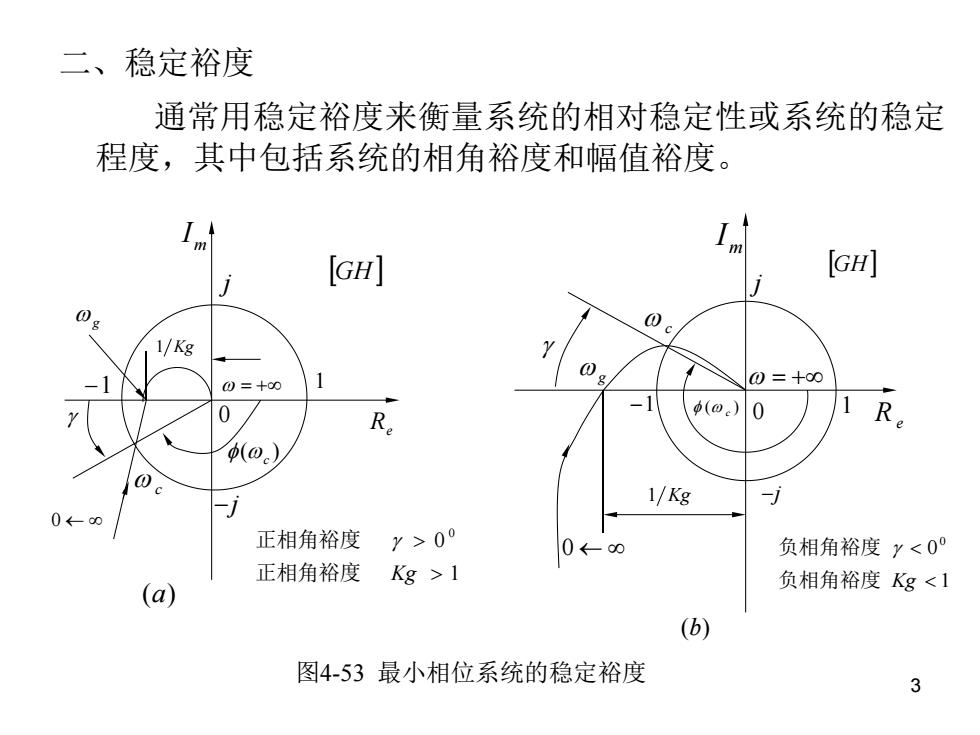
二、稳定裕度 通常用稳定裕度来衡量系统的相对稳定性或系统的稳定 程度,其中包括系统的相角裕度和幅值裕度。 m m [GH] [GH] 0g c 1/Kg 0 0=+00 0=+00 0 1 R。 (o)0 R (0) 1/Kg -j 0←-0 正相角裕度 Y>00 0←0 负相角裕度y<0 正相角裕度 Kg >1 负相角裕度Kg<1 (a) (b) 图4-53最小相位系统的稳定裕度 3
3 二、稳定裕度 通常用稳定裕度来衡量系统的相对稳定性或系统的稳定 程度,其中包括系统的相角裕度和幅值裕度。 图4-53 最小相位系统的稳定裕度 ( ) c 0 jj 1 g 0 1 Kg 1 m I R e c GH 1 0 0 负相角裕度 Kg 负相角裕度 (b) m I Re ( ) c GH 1 Kg g 0 j j 1 1 1 0 0 正相角裕度 Kg 正相角裕度 (a) 0 c

(一)相角裕度 如图5一53所示,我们把GH平面上的单位圆与系统开环频率特性曲 线的交点频率⊙。称为幅值穿越频率或剪切频率,它满足 G(j0c)H(j0c)=1(0≤0。≤+0) (4-124) 所谓相角裕度是指幅值穿越频率所对应的相移 (o月-180角的差值, 即 y=φ(0e)-(-180)=p(o)+1800 (4-125) 对于最小相位系统,如果相角裕度 y>系统是稳定的(图4-53a)), 且值愈大,系统的相对稳定性愈好。如果相角裕度 ,系统则不 稳每(图4-53(b))。当 时,系统的开环频率得性曲线穿过 点,系统处于临界稳定状盛。 (-1,j0) 相角裕度的含义使系统达到稳定的临界状态时的开环频率特性的相角 p(o)=∠G(j0)H(j0)减小(对应稳定系统)或增加(对应不稳定系统) 的数值。 4
4 所谓相角裕度是指幅值穿越频率所对应的相移 与-1800角的差值, 即 (4-125) 对于最小相位系统,如果相角裕度 ,系统是稳定的(图4-53a)), 且 值愈大,系统的相对稳定性愈好。如果相角裕度 ,系统则不 稳定( 图 4-53(b))。当 时,系统的开环频率特性曲线穿过 点,系统处于临界稳定状态。 ( ) c 0 0 ( ) ( 180 ) ( ) 180 c c 0 0 0 0 0 0 ( 1, j ) 相角裕度的含义 使系统达到稳定的临界状态时的开环频率特性的相角 减小(对应稳定系统)或增加(对应不稳定系统) 的数值。 (一) 相角裕度 如图5—53所示,我们把GH平面上的单位圆与系统开环频率特性曲 线的交点频率 称为幅值穿越频率或剪切频率,它满足 ( ) ( ) 1(0 ) c c c G j H j c (4-124) ( ) ( ) ( ) c c c G j H j

二) 幅值裕度 如图4-53所示,我们把系统的开环频率特性曲线与GH平面负实轴的 交点频率称为相位穿越频率®。,显然它应满足 (4-126) ∠G(j0.)H(j0.)=-180°(0≤0。≤+0) 所谓幅值裕度Kg是指相位穿越频率所对应的开环幅频特性的倒数值,即 1 K&- G(jo)H(jo) (4-127) 对于最小相位系统,当幅值裕度Kg>1(G(jog)H(jo)<1),系统是稳 定的(图4-53(a)),且Kg值愈大,系统的相对稳定性愈好。如果幅值裕 度K。<1,(G(0g)H(j0>1),系统则不稳定(图4-53(b)。当Kg=1时, 系统的开环频率特性曲线穿过 (-1,点。是临界稳定状态。可见,求出 系统的幅值裕度Kg后,便可根据Kg值的大小来分析最小相位系统的稳定 性和稳定程度。 5
5 (二) 幅值裕度 如图4-53所示,我们把系统的开环频率特性曲线与GH平面负实轴的 交点频率称为相位穿越频率 ,显然它应满足 (4-126) 所谓幅值裕度Kg是指相位穿越频率所对应的开环幅频特性的倒数值,即 (4-127) ( ) ( ) 180 (0 ) 0 G j g H j g g ( ) ( ) 1 G j H j K g 对于最小相位系统,当幅值裕度Kg>1( ),系统是稳 定的(图4-53(a)),且Kg值愈大,系统的相对稳定性愈好。如果幅值裕 度 ,( ),系统则不稳定( 图4-53(b))。当Kg=1时, 系统的开环频率特性曲线穿过 点。是临界稳定状态。可见,求出 系统的幅值裕度 Kg 后,便可根据 Kg值的大小来分析最小相位系统的稳定 性和稳定程度。 G( j g )H ( j g ) 1 Kg 1 G( j g )H ( j g ) 1 ( 1 , j ) g