
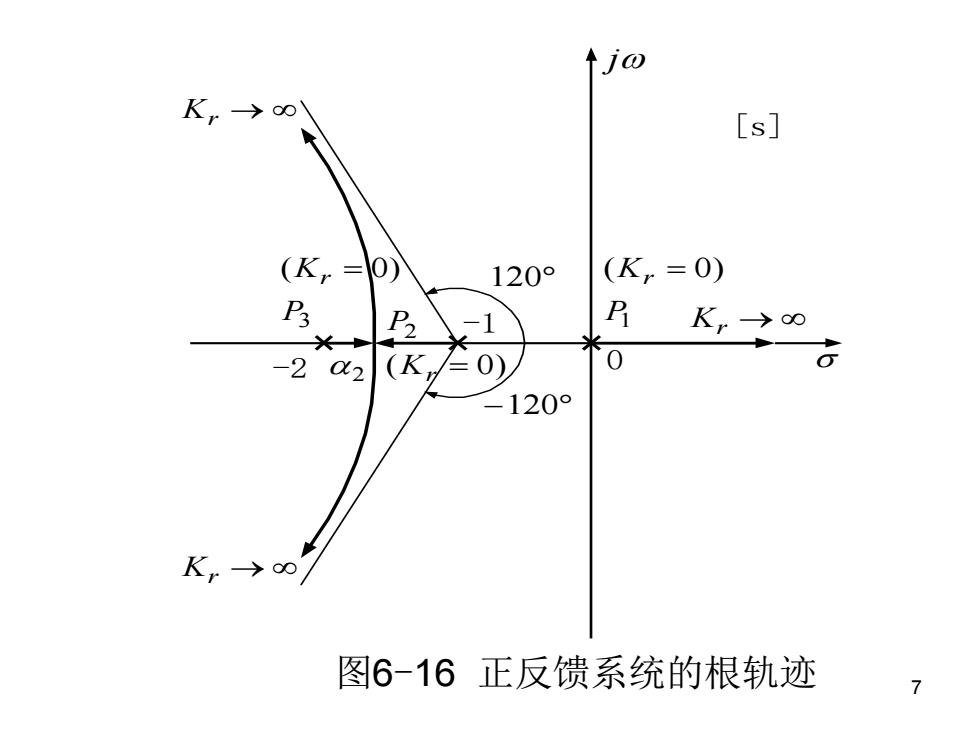
本例无共轭复数开环零、极点,不存在起始 角和终止角问题,根轨迹与虚轴也无交点。本例 的根轨迹如图6-16所示。由图6-16可看出,三 条根轨迹中,有一条从起点到终点全部位于S平 面右半部,这就意味着无论K,为何值,系统都 存在S平面右半部的闭环极点,该正反馈系统总 是不稳定的。而有相同开环传递函数的负反馈系 统(例6-7,图6-1),它的临界轨迹增益 即幽c=6时系统是不稳定的,当 K,<6时系统是稳定的。由此可知,在开环传递 函数相同的情况下,负反馈系统的稳定性比正反 馈系统好。 6
6 本例无共轭复数开环零、极点,不存在起始 角和终止角问题,根轨迹与虚轴也无交点。本例 的根轨迹如图6-16所示。由图6-16可看出,三 条根轨迹中,有一条从起点到终点全部位于S平 面右半部,这就意味着无论 为何值,系统都 存在S平面右半部的闭环极点,该正反馈系统总 是不稳定的。而有相同开环传递函数的负反馈系 统(例6-7,图6-1l),它的临界轨迹增益 , 即当 时系统是不稳定的,当 时系统是稳定的。由此可知,在开环传递 函数相同的情况下,负反馈系统的稳定性比正反 馈系统好。 Kr 6 Kr 6 Kr Krc = 6
↑jω K,> [s] (K,=O) 120° (Kx=0) Ps -1 R K -22 (K0) 0 120° Kr→ 图6-16正反馈系统的根轨迹 7
7 [s] j 1( 0) PKr =Kr → 0 120 −120 -1 Kr → Kr → 3 ( 0) PKr = ( 0) 2Kr = P -2 2图 6 -16 正反馈系统的根轨迹

三非最小相位系统的根轨迹 所谓非最小相位系统,是指那些在S平面右 半部有开环极点和(或开环零点)的控制系统。 所有开环零点和极点都位于S平面左半部的系统 叫最小相位系统。本章前面介绍的示例都是最小 相位系统。非最小相位系统一词源于对系统频率 特性的描述,即在正弦信号的作用下,具有相同 幅频特性的系统(或环节),最小相位系统的相 位移最小,而非最小相位系统的相位移大于最小 相位系统的相位移。 8
8 三 非最小相位系统的根轨迹 所谓非最小相位系统,是指那些在S平面右 半部有开环极点和(或开环零点)的控制系统。 所有开环零点和极点都位于S平面左半部的系统 叫最小相位系统。本章前面介绍的示例都是最小 相位系统。非最小相位系统一词源于对系统频率 特性的描述,即在正弦信号的作用下,具有相同 幅频特性的系统(或环节),最小相位系统的相 位移最小,而非最小相位系统的相位移大于最小 相位系统的相位移

例6-12已知负反馈系统的开环传递函数为 K(s+1) G(s)H(s)= s(S-1)(s2+2s+2) 试绘制该系统的根轨迹图。 解 该系统有一位于S平面右半部的开环极点 (P2=1),是非最小相位系统。系统特征方程 的最高阶次是4,由规则一、二知该系统有四条 连续且对称于实轴的根轨迹。四条根轨迹的起点 分别是它的四个开环极点, p1=0p2=1p3=-1+j1p4=-1-jl 9
9 例6-12 已知负反馈系统的开环传递函数为 试绘制该系统的根轨迹图。 解 该系统有一位于S平面右半部的开环极点 ( ),是非最小相位系统。系统特征方程 的最高阶次是4,由规则一、二知该系统有四条 连续且对称于实轴的根轨迹。四条根轨迹的起点 分别是它的四个开环极点, p 1 2 = s(s 1)(s 2s 2) K (s 1) G(s)H(s) 2 r − + + + = p 0 1 = p 1 2 = p3 = −1+ j1 p4 = −1− j1

根轨迹的一个终点是它的有限开环零点, 即Z1=-1,其余三个终点均在无穷远处(无 限零点)。 由规则四知,根轨迹的三条渐近线与实轴 的交点为 m Σ(P)-Σ(Z) 0a= i=1 j=1 =0 n-m 渐近线与实轴正方向的夹角分别是60°(k=0): 180°(k=1)和-60°(k=2)。 10
10 根轨迹的一个终点是它的有限开环零点, 即 ,其余三个终点均在无穷远处(无 限零点)。 由规则四知,根轨迹的三条渐近线与实轴 的交点为 渐近线与实轴正方向的夹角分别是60°(k=0), 180°(k=1)和-60°(k=2)。 z 1 1 = − 0 n m (P ) (Z ) m j 1 j n i 1 i a = − − = = =