
历些毛子代枝大学 逆向归纳法 XIDIAN UNIVERSITY 一个例子 D 策略式(收益矩阵)表述 见右下图。 B (2,2) A2 *可见,它有两个纳什均衡: R (3,1)和(2,2)。 (3.1) (0,0) 如果A选择U,B的信息集 B 就不可达,即B的信息集 L R 不在均衡路径上。 U 2,2 2,2 D 3,1 0,0
逆向归纳法 一个例子 策略式(收益矩阵)表述 见右下图。 可见,它有两个纳什均衡: (3, 1) 和 (2, 2)。 如果A选择U, B的信息集 就不可达, 即B的信息集 不在均衡路径上。 L R U 2, 2 2, 2 D 3, 1 0, 0 A B

历安毛子种枚大学 逆向归纳法 XIDIAN UNIVERSITY *逆向归纳法(Backward Induction)是求 解动态博弈纳什均的最简便方法。在求 解动态博弈纳什均斯时,从最后一个子博弈 开始逆推上去,这就是逆向归纳法。所以逆 向归纳法就是从动态博弈的最后一个阶段 或最后一个子博弈开始,逐步向前倒推以求 解动态博弈均的方法
逆向归纳法 逆向归纳法(Backward Induction)是求 解动态博弈纳什均衡的最简便方法。在求 解动态博弈纳什均衡时,从最后一个子博弈 开始逆推上去,这就是逆向归纳法。所以逆 向归纳法就是从动态博弈的最后一个阶段 或最后一个子博弈开始,逐步向前倒推以求 解动态博弈均衡的方法
历安毛子代枚大学 逆向归纳法 XIDIAN UNIVERSITY *从博弈的最后一个阶段开始分析,若B选择L获利 1,选择R获利0,因此B选L。 倒退到第一阶段,A选U获利2,选D获利取决于B 的选择。 *但A知道B是理性的,一旦 到达第二阶段,B肯定选择 D L,从而,A获利3。因此, A应该选择D。 B (2,2) A2 因此,D,L)是纯策略 R 纳什均衡。 (3.1) (0,0)
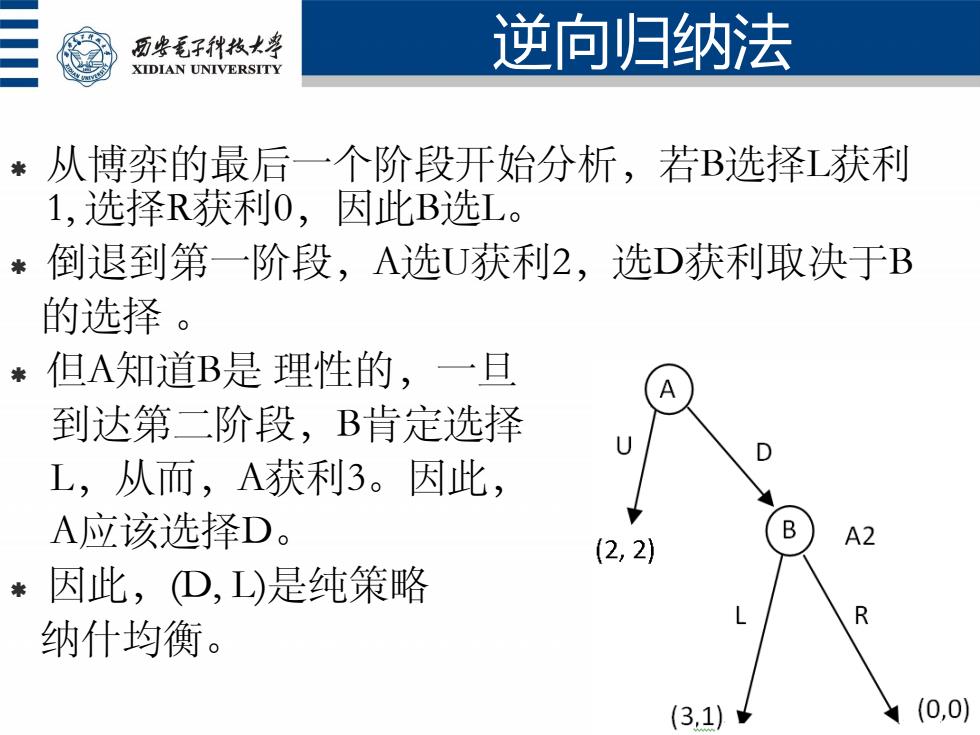
从博弈的最后一个阶段开始分析,若B选择L获利 1, 选择R获利0,因此B选L。 倒退到第一阶段,A选U获利2,选D获利取决于B 的选择 。 但A知道B是 理性的,一旦 到达第二阶段,B肯定选择 L,从而,A获利3。因此, A应该选择D。 因此,(D, L)是纯策略 纳什均衡。 逆向归纳法

历安毛子代枚大等 与策略式分析的比较 XIDIAN UNIVERSITY 逆向归纳法实际上是严格 D 下策反复删去法在扩展式 描述的动态博弈中的应用2,2) B A2 *逆向归纳法不适合无限 R 博弈。 *逆向归纳法不适合不 (3,1) (0,0) 完美信息博弈。 B L R 逆向归纳法剔出了非 U 2,2 2,2 理性的均衡策略。 D 3,1 0,0
与策略式分析的比较 逆向归纳法实际上是严格 下策反复删去法在扩展式 描述的动态博弈中的应用。 逆向归纳法不适合无限 博弈。 逆向归纳法不适合不 完美信息博弈。 逆向归纳法剔出了非 理性的均衡策略。 L R U 2, 2 2, 2 D 3, 1 0, 0 A B

历安毛子代枚大学 逆推归纳法:海盗分赃 XIDIAN UNIVERSITY 5个海盗抢来100个金币,大家决定分赃的 方式是:由海盗一提出一种分配方案,如果同 意该方案的人数达到半数,则该提议通过并实 施。否则该提议人将被扔进大海,然后由接下 来的海盗重复提议过程。 假定每个人都绝顶聪明,也不相互合作,并 且极度自私,那么第一个海盗该如何提议
逆推归纳法:海盗分赃 5个海盗抢来100个金币,大家决定分赃的 方式是:由海盗一提出一种分配方案,如果同 意该方案的人数达到半数,则该提议通过并实 施。否则该提议人将被扔进大海,然后由接下 来的海盗重复提议过程。 假定每个人都绝顶聪明,也不相互合作,并 且极度自私,那么第一个海盗该如何提议