
第四节线性系统的稳态误差分析计算 控制系统的稳态误差,是控制精度(准确度) 的一种度量,是控制系统的稳态性能指标。在实 际系统中,引起稳态误差的因素是多种多样的。 本节仅仅讨论线性系统由于系统结构、参数 及输入信号形式不同所引起的稳态误差。 一,系统误差及稳态误差的概念 实际物理系统从其主反馈通道来看分为单位 反馈和非单位反馈两种基本结构形式如图3.27(a) 及(b)所示
第四节 线性系统的稳态误差分析计算 控制系统的稳态误差,是控制精度(准确度) 的一种度量,是控制系统的稳态性能指标。在实 际系统中,引起稳态误差的因素是多种多样的。 本节仅仅讨论线性系统由于系统结构、参数 及输入信号形式不同所引起的稳态误差。 一. 系统误差及稳态误差的概念 实际物理系统从其主反馈通道来看分为单位 反馈和非单位反馈两种基本结构形式如图3.27(a) 及(b)所示
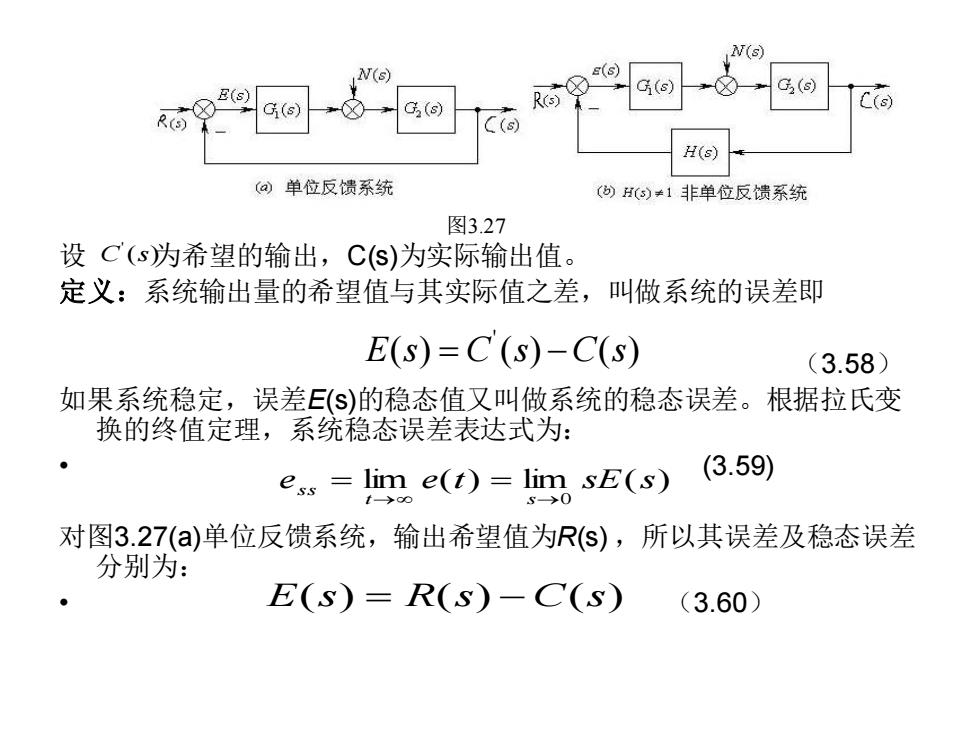
N(s N(s) (s) G,(s) (s (s H(s) @单位反馈系统 ()(s)≠1非单位反馈系统 图3.27 设C(s为希望的输出,Cs)为实际输出值。 定义:系统输出量的希望值与其实际值之差,叫做系统的误差即 E(s)=C(s)-C(s) (3.58) 如果系统稳定,误差E($)的稳态值又叫做系统的稳态误差。根据拉氏变 换的终值定理,系统稳态误差表达式为: ess=l。e(t)=limsE(s) (3.59) 对图3.27(a)单位反馈系统,输出希望值为R(s),所以其误差及稳态误差 分别为: E(S)=R(S)一C(S) (3.60)
设 为希望的输出,C(s)为实际输出值。 定义:系统输出量的希望值与其实际值之差,叫做系统的误差即 (3.58) 如果系统稳定,误差E(s)的稳态值又叫做系统的稳态误差。根据拉氏变 换的终值定理,系统稳态误差表达式为: • (3.59) 对图3.27(a)单位反馈系统,输出希望值为R(s) ,所以其误差及稳态误差 分别为: • (3.60) ' E s C s C s ( ) ( ) ( ) = − 图3.27 lim ( ) lim ( ) 0 e e t sE s t s s s → → = = E s R s C s ( ) ( ) ( ) = − ' C s( )

ess=lim sE(s)=lim s[R(s)-C(s)] 50 1 =ling$1+G(s) R(S) 式中,G(s)=G(s)G2(s)。 对图3.27(b)所示非单位反馈系统,将其进行结构等效变换成 单位反馈如图3.28所示。则其输出希望值为(s5,所 以其误差及稳态误差分别为: Es=R(-C()= 1R(S)-C(S) (3.62) H(s) 1 es =lim E(s)=lims- R(s) (3.63) 0°1+G(s) 1 lims 1R(S) 361+Gx(s)H(s) 式中, G(s)=G(s)G(s)H(s)
式中, 。 对图3.27(b)所示非单位反馈系统,将其进行结构等效变换成 单位反馈如图3.28所示。则其输出希望值为 ,所 以其误差及稳态误差分别为: (3.62) (3.63) 式中, 0 0 lim ( ) lim [ ( ) ( )] ss s s e sE s s R s C s → → = = − 0 1 lim ( ) s 1 ( ) k s R s → G s = + ( ) ( ) ( ) 1 2 G s G s G s k = ' 1 ( ) ( ) ( ) R s R s H s = ' 1 ( ) ( ) ( ) ( ) ( ) ( ) E s R s C s R s C s H s = − = − ' 0 0 1 lim ( ) lim ( ) 1 ( ) ss s s k e E s s R s → → G s = = + 0 1 1 lim ( ) 1 ( ) ( ) s k s R s → G s H s = + ( ) ( ) ( ) ( ) 1 2 G s G s G s H s k =
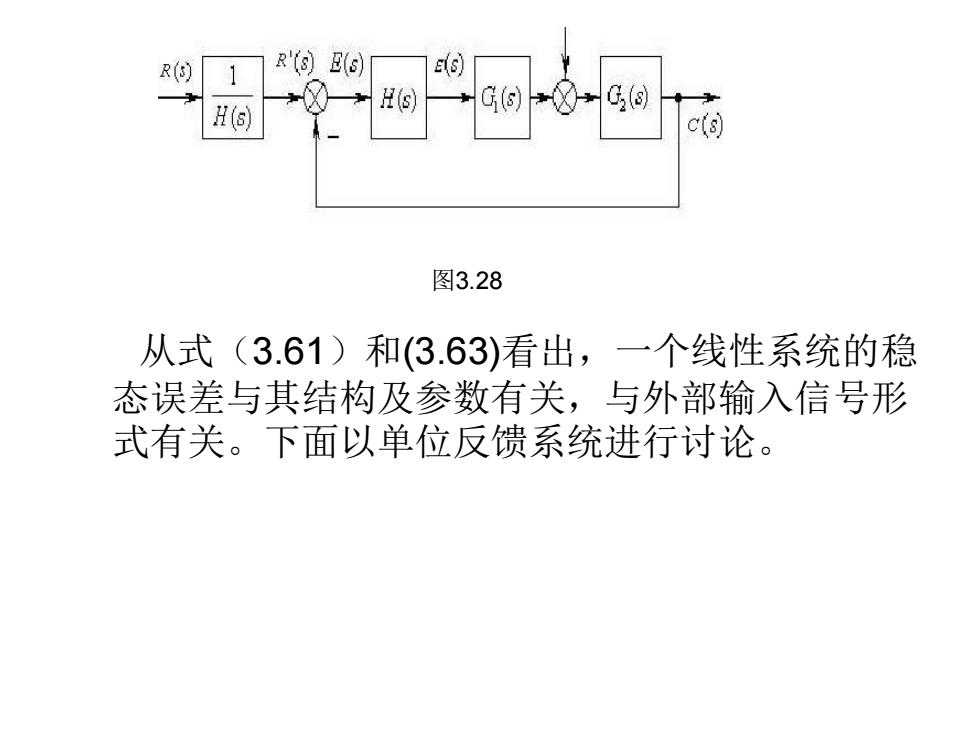
R(s) R'(s)E(s) G(s H(s) 图3.28 从式(3.61)和(3.63)看出,一个线性系统的稳 态误差与其结构及参数有关,与外部输入信号形 式有关。下面以单位反馈系统进行讨论
从式(3.61)和(3.63)看出,一个线性系统的稳 态误差与其结构及参数有关,与外部输入信号形 式有关。下面以单位反馈系统进行讨论。 图3.28

二.系统结构类型及开环增益 设单位反馈系统的开环传递函数为: G)= K(5+1).....(s+1)K(s+z).....(s+zm) S"(Ts+1)…(Tn-vS+I)S"(s+p)…(s+P-v) (3.64) G(s) K 式中,G(-+D…5+D当0,G0=l。 (Ts+1)…(Tmvs+'1) 从式(3.61)和(3.64)看出,系统稳态误差与其开环传递函数 有关,其实仅与G(s)中积分环节和K有关
二.系统结构类型及开环增益 设单位反馈系统的开环传递函数为: (3.64) 式中, ,当s→0,G0(0)=1。 从式(3.61)和(3.64)看出,系统稳态误差与其开环传递函数 有关,其实仅与Gk(s)中积分环节和K有关。 ( ) ( ) ( ) ( ) ( 1) ( 1) ( 1) ( 1) ( ) 1 * 1 1 − + − + + + = + + + + = n m n m k S s p s p K s z s z S T s T s K s s G s ( ) 0 G s S K = ( 1) ( 1) ( 1) ( 1) ( ) 1 1 0 + + + + = − T s T s s s G s n m