
§4-4 奈奎斯特稳定判据 第三章已经介绍,闭环控制系统的稳定性由系统特征方 程根的性质唯一确定。对于三阶以下系统,解出特征根就能判 断系统是否稳定。三阶以上的高阶系统,求解特征根通常都很 困难,前面介绍了两种判别系统稳定性的方法,基于特征方程 的根与系数关系的劳斯判据和根轨迹法。 奈奎斯特(Nyquist)稳定判据(简称奈氏判据)是判断 系统稳定性的又一重要方法。它是将系统的开环频率特性 G(jo)H(jo)与复函数F(s)=1+G(s)H(s)位于S平面右半部的零、 极点数目联系起来的一种判据。奈氏判据是根据系统的开环频 率特性判断系统稳定性的一种图解法。由于系统的开环特性可 用解析法或实验法获得,因此,应用奈氏判据分析系统的稳定 性即方便又实用。奈氏判据还有助于建立相对稳定性的概念。 1
1 § 4-4 奈奎斯特稳定判据 第三章已经介绍,闭环控制系统的稳定性由系统特征方 程根的性质唯一确定。对于三阶以下系统,解出特征根就能判 断系统是否稳定。三阶以上的高阶系统,求解特征根通常都很 困难,前面介绍了两种判别系统稳定性的方法,基于特征方程 的根与系数关系的劳斯判据和根轨迹法。 奈奎斯特(Nyquist)稳定判据(简称奈氏判据)是判断 系统稳定性的又一重要方法。它是将系统的开环频率特性 与复函数 位于S平面右半部的零、 极点数目联系起来的一种判据。奈氏判据是根据系统的开环频 率特性判断系统稳定性的一种图解法。由于系统的开环特性可 用解析法或实验法获得,因此,应用奈氏判据分析系统的稳定 性即方便又实用。奈氏判据还有助于建立相对稳定性的概念。 G( j)H( j) F(s) =1+ G(s)H(s)

一、幅角定理 幅角定理又称映射定理,它是建立在复变函数理论基础上的。简要地介绍幅角 定理: 设有一复变函数 F()=1+G(S)H(S) (4-105) 称之为辅助函数,其中G(s)H(s)是系统的开环传递函数。 通常可写成如下形式 G(s)Hs)=bms”+b-1sm1+.+bs+b, (s-p1)s-p2)..(s-pm) (4-106) 式中p(=1,2,,n)是系统的开环极点,将式(4-106)代入式(4-105)得 F(s)=k(s-31s-22).(s-2n) (4-107) (s-p1)s-P2).(s-Pn) 比较式(4一107)和式(4一106)可知,辅助函数F(s)的零点Z,亿=1,2,,n)等于系 统闭环传递函数的极点,即系统特征方程1+G(s)H⑤)=0的根。因此,如果辅助函数F(s) 的零点都具有负的实部,即都位于$平面的左半部,系统就是稳定的,否则系统便不稳 定。 2
2 一、幅角定理 幅角定理又称映射定理,它是建立在复变函数理论基础上的。简要地介绍幅角 定理: 设有一复变函数 (4-105) 称之为辅助函数,其中 是系统的开环传递函数. F(s) =1+ G(s)H(s) G(s)H(s) 通常可写成如下形式 (4-106) 式中 是系统的开环极点,将式(4-106)代入式(4-105)得 (4-107) 比较式(4—107)和式(4—106)可知,辅助函数 的零点 等于系 统闭环传递函数的极点,即系统特征方程 的根。因此,如果辅助函数 的零点都具有负的实部,即都位于S平面的左半部,系统就是稳定的,否则系统便不稳 定。 ( )( ) ( ) ( ) ( ) 1 2 1 0 1 1 n m m m m s p s p s p b s b s b s b G s H s − − − + ++ + = − − ( )( ) ( ) ( )( ) ( ) ( ) 1 2 1 2 n n s p s p s p k s z s z s z F s − − − − − − = F(s) Z (i 1,2, ,n) i = 1+ G(s)H(s) = 0 F(s) ( 1,2, , ) p j n j =

(一)S平面与F(s)平面的映射关系 假设复变函数F(s)为单值函数,且除了S平面上有限的奇 点外,处处都为连续的正则函数,也就是说F(s)在S平面上除 奇点外处处解析,那么,对于S平面上的每个解析点,在F(s) 平面上必有一点(称为映射点)与之对应。 例如,当系统的开环传递函数为 G(S)H(s)= s(S+1) 则其辅助函数是 F(s)=1+G(s)H(s)= s2+s+1 s(s+1) 除奇点s'=0和s”=-1外,在S平面上任取一点,如 S1=1+2 则 Fs,)=0+/2)+1+2)+1=0.95-j0.15 (1+2)(1+12+1) 3
3 假设复变函数 为单值函数,且除了S平面上有限的奇 点外,处处都为连续的正则函数,也就是说 在S平面上除 奇点外处处解析, 那么,对于S平面上的每个解析点,在 平面上必有一点(称为映射点)与之对应。 例如,当系统的开环传递函数为 则其辅助函数是 除奇点 和 外,在S平面上任取一点,如 则 F(s) F(s) ( 1) 1 ( ) ( ) + = s s G s H s ( 1) 1 ( ) 1 ( ) ( ) 2 + + + = + = s s s s F s G s H s s = 0 s = −1 (一)S平面与 平面的映射关系 F(s) s1 =1+ j2 0.95 0.15 (1 2)(1 2 1) (1 2) (1 2) 1 ( ) 2 1 j j j j j F s = − + + + + + + + = F(s)
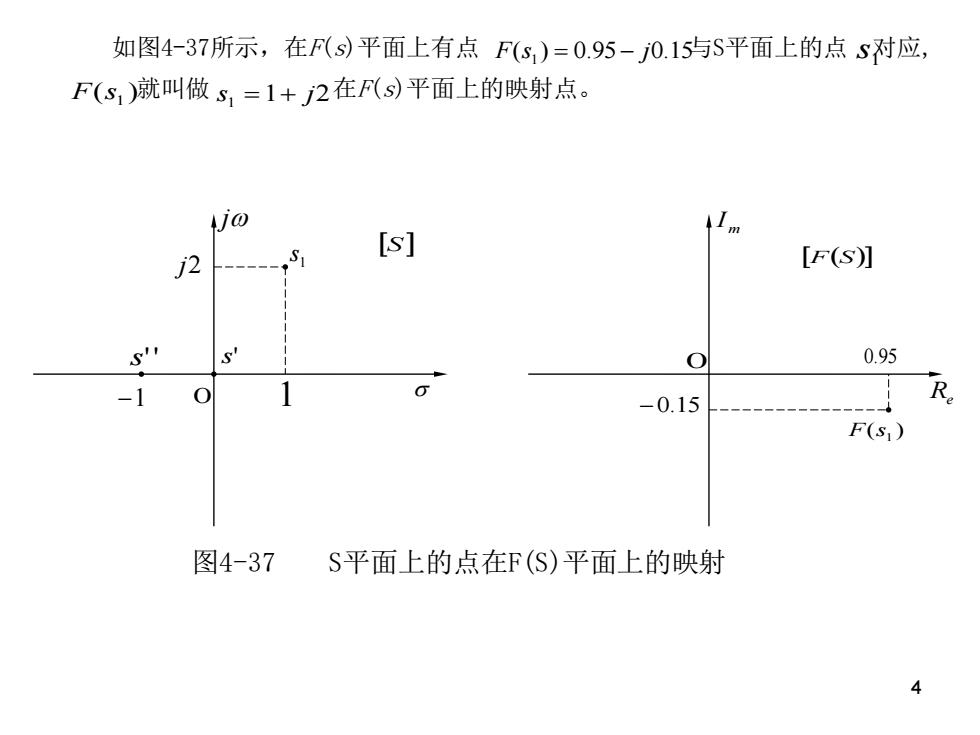
如图4-37所示,在F(s)平面上有点F(s)=0.95-j0.15与S平面上的点s对应, F(s,)就叫做s,=1+2在F(s)平面上的映射点。 S [S] 2 [F(S] O 0.95 -0.15 R F(S1) 图4-37 S平面上的点在F(S)平面上的映射 4
4 如图4-37所示,在F(s)平面上有点 与S平面上的点 对应, 就叫做 在F(s)平面上的映射点。 F(s1 ) = 0.95 − j0.15 F(s1 ) s1 =1+ j2 1 s j j2 1 s s' 0 −1 s'' 1 S m I 0 Re ( )1 F s F(S) −0.15 0.95 图4-37 S平面上的点在F(S)平面上的映射
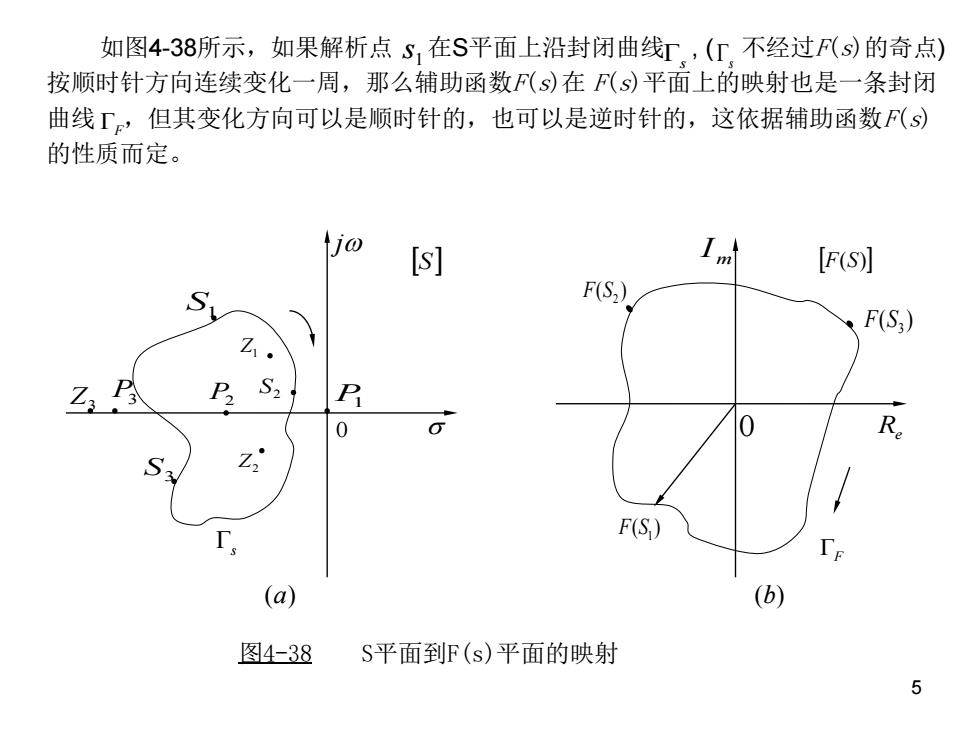
如图4-38所示,如果解析点S,在S平面上沿封闭曲线T,(上.不经过F(s)的奇点) 按顺时针方向连续变化一周,那么辅助函数F(s)在F(s)平面上的映射也是一条封闭 曲线『,但其变化方向可以是顺时针的,也可以是逆时针的,这依据辅助函数F(s) 的性质而定。 [s] [F(S] F(S,) F(S) Z S P 0 0 Re F(S) Te (a) (b) 图4-38 S平面到F(s)平面的映射 5
5 如图4-38所示,如果解析点 在S平面上沿封闭曲线 , ( 不经过F(s)的奇点) 按顺时针方向连续变化一周,那么辅助函数F(s)在 F(s)平面上的映射也是一条封闭 曲线 ,但其变化方向可以是顺时针的,也可以是逆时针的,这依据辅助函数F(s) 的性质而定。 1 s F s s j S P2 P1 S1 S2 S3 P3 Z1 Z2 Z3 0 (a) m I F(S) Re ( )1 F S ( )2 F S ( )3 F S 0 图4-38 S平面到F(s)平面的映射 (b) s F