
第六章 第二节 定积分在儿何学上的应用 一、平面图形的面积 二、体积 三、平面曲线的弧长 HIGH EDUCATION PRESS 机动目录上页下页返回结束
第二节 机动 目录 上页 下页 返回 结束 定积分在几何学上的应用 第六章 一、平面图形的面积 二、体积 三、平面曲线的弧长
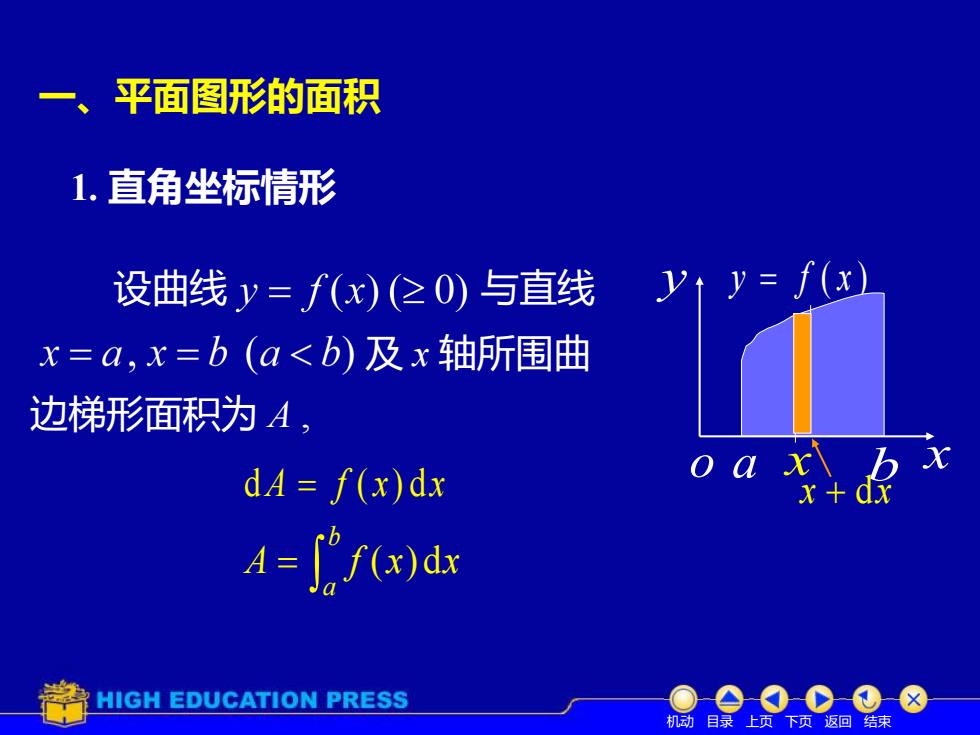
一、平面图形的面积 1.直角坐标情形 设曲线y=f(x)(20)与直线 y↑y=f(x) x=a,x=b(a<b)及x轴所围曲 边梯形面积为A, d4=f(x)dx =()dx HIGH EDUCATION PRESS 机动目录上页下页返回结束
1. 直角坐标情形 设曲线 与直线 及 x 轴所围曲 dA = f ( x) dx o a b x y y = f ( x ) x x + dx A f x x b a ( ) d = 机动 目录 上页 下页 返回 结束 边梯形面积为 A , 一、平面图形的面积

设曲线y=(x),y=f(x) vy=(x)y=f2(x) 与直线x=a,x=b(a<b) 及x轴所围曲边梯形面积为A axx+dx bx dA=(x)-f(x)dx 4=["f(x)-f2(x)dx HIGH EDUCATION PRESS 机动目 绿上页下页返回结束
1 2 d ( ) ( ) d A f x f x x = − 机动 目录 上页 下页 返回 结束 y o a b x ( ) 2 ( ) y = f x 1 y = f x A f x f x x b a ( ) ( ) d = 1 − 2 x x + d x 设曲线 与直线 及 x 轴所围曲边梯形面积为 A
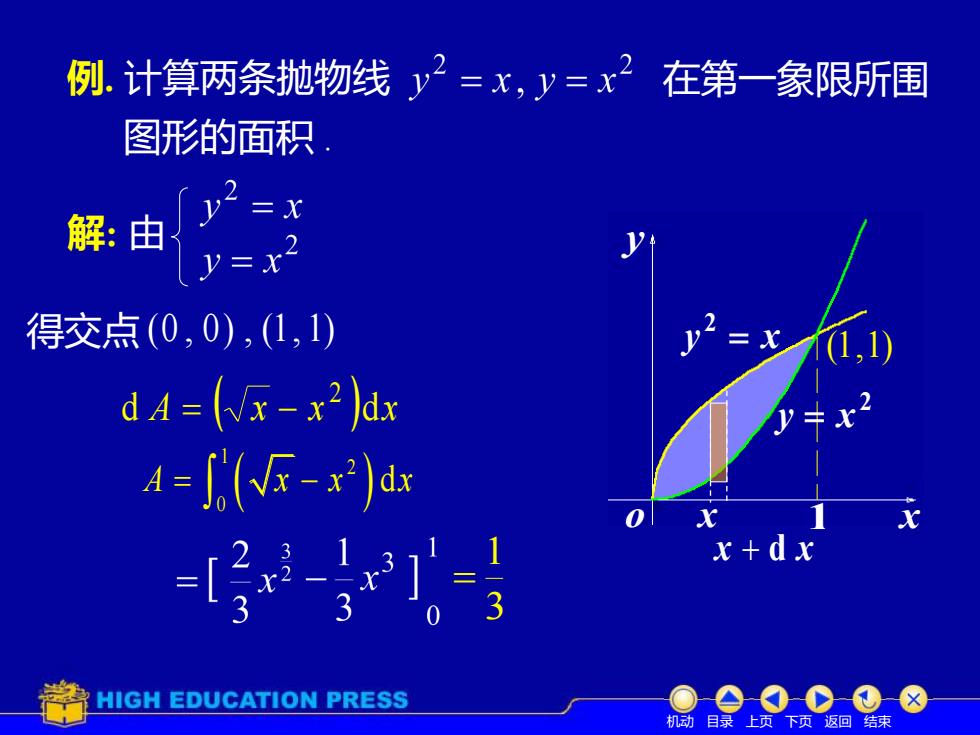
例.计算两条抛物线 y2=x,y=x2在第一象限所围 图形的面积 解由/y y-x 得交点(0,0),(1,1) d4=(x-x2ax 4=(G-x)a x+dx HIGH EDUCATION PRESS 机动目录上页下页返回结束
例. 计算两条抛物线 在第一象限所围 图形的面积 . x y = x 2 o y 2 y = x x x + d x 解: 由 得交点 (0 , 0) , (1, 1) (1,1) 1 d A ( x x )dx 2 = − 3 1 = 机动 目录 上页 下页 返回 结束 ( ) 1 2 0 A x x x = − d

例.计算抛物线y2=2x与直线y=x-4所围图形 的面积 解:由 y2=2x 得交点 y=x-4 y2=2x (8.4 (2,-2),(8,4) 为简便计算,选取y作积分变量, 则有 A=2(y+4-2)dy =[5y2+4y-y3]12=18 HIGH EDUCATION PRESS 机动目影 上页下页返回结束
x y 2x 2 = o y y = x − 4 例. 计算抛物线 y 2x 2 = 与直线 的面积 . 解: 由 得交点 (2 , − 2) , (8 , 4) (8 , 4) d A ( y 4 y ) dy 2 2 1 = + − = 18 y = x − 4 所围图形 (2 , − 2) 为简便计算, 选取 y 作积分变量, 则有 y y + d y − = 4 2 A 机动 目录 上页 下页 返回 结束