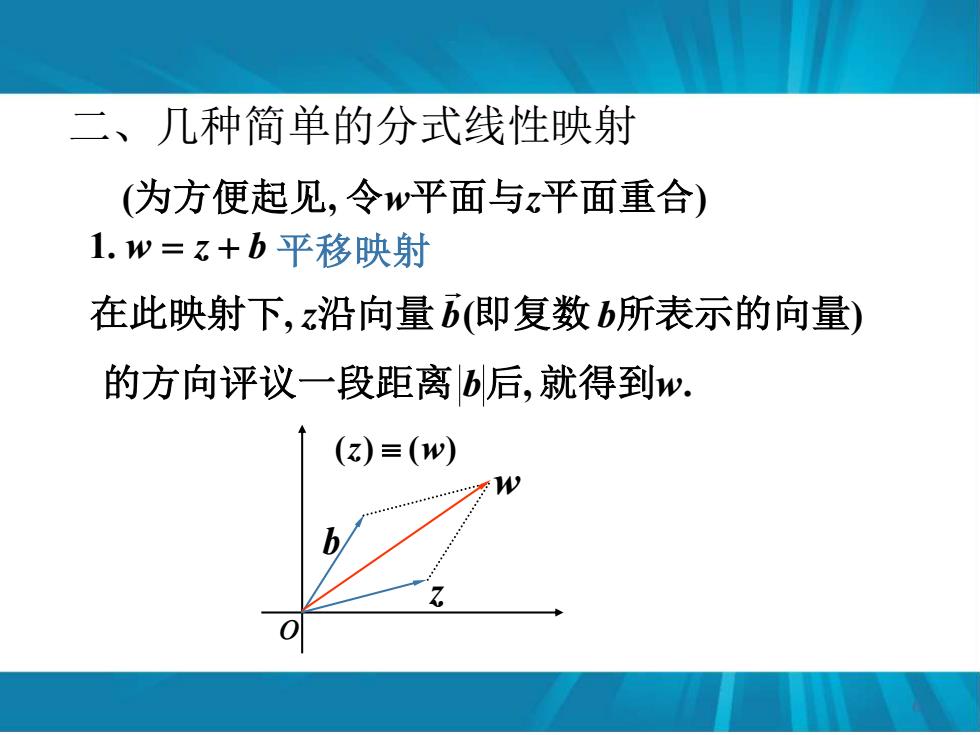
二、几种简单的分式线性映射 (为方便起见,令w平面与z平面重合) 1.w=z+b平移映射 在此映射下,z沿向量(即复数b所表示的向量) 的方向评议一段距离b后,就得到w. (z)≡(w)
二、几种简单的分式线性映射 1. w = z + b 平移映射 (为方便起见, 令w平面与z平面重合) 在此映射下, z沿向量b(即复数b所表示的向量) 的方向评议一段距离 b后,就得到w. o (z) (w) z b w 6
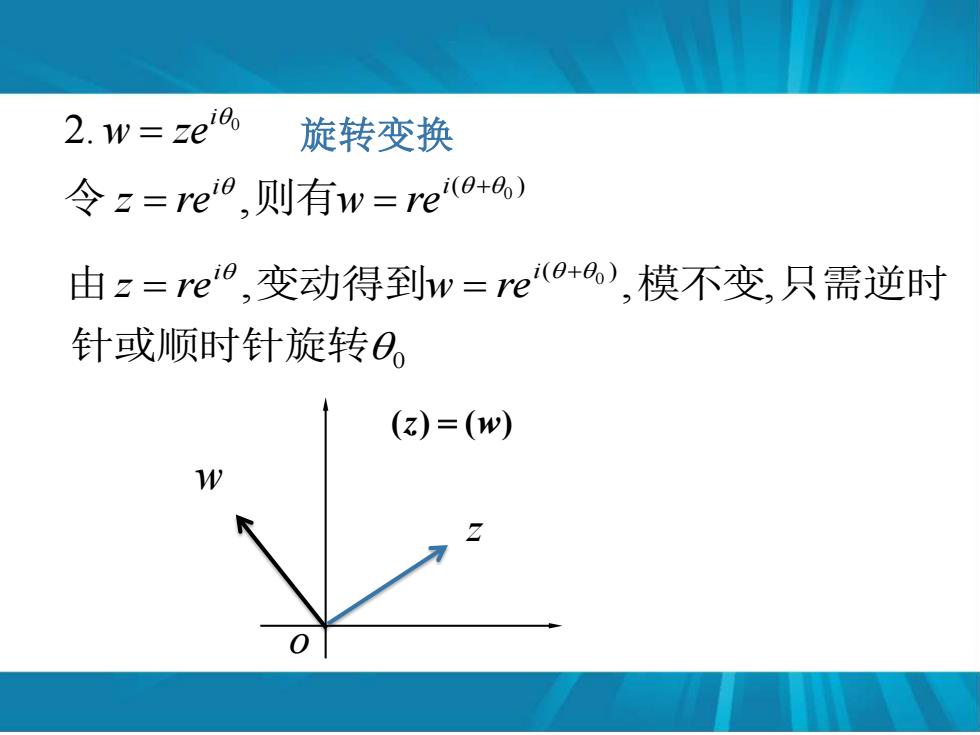
2.w=ze8, 旋转变换 令z=re,则有w=re0+8) 由z=re0,变动得到w=re(a+a),模不变,只需逆时 针或顺时针旋转8, (z)=(w)
0 2. i w = ze 旋转变换 ( ) 0 , + = = i i 令 z re 则有w re o (z) = (w) z w 0 ( ) , , , 0 针或顺时针旋转 由z = re i 变动得到w = re i + 模不变 只需逆时
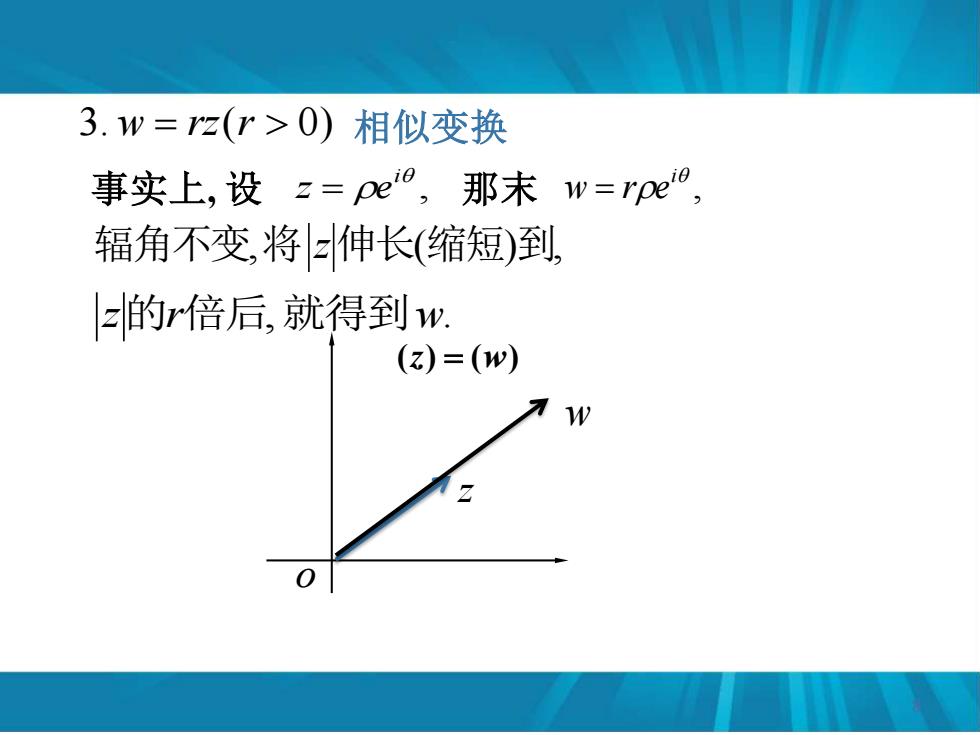
3.w=z(r>0)相似变换 事实上,设z=pe,那末w=rpe0, 辐角不变,将z伸长(缩短)到, z的r倍后,就得到w: (Z)=(w)
3. w = rz(r 0) 相似变换 事实上, 设 , i z = e 那末 , i w = r e 辐角不变,将 z伸长(缩短)到, z的r倍后,就得到w. o (z) = (w) 8 z w

4.w=- 反演映射 此映射可进一步分解为 1 W1= w=W 欲由点z作出点w,可考虑如下作图次序: →7→ 关于横轴对称 关键:在几何上如何由z→w,?
关于横轴对称 z w 1 4. = 反演映射 此映射可进一步分解为 , 1 1 z w = w = w1 欲由点z作出点w, 可考虑如下作图次序: z → z → w1 → w 关键: 在几何上如何由z → w1 ? 9