
第七章多元函数积分学
21 第七章 多元函数积分学

第七章多元函数积分学 (2)若积分区域D关于y轴对称,x,y)为x的奇偶函数,则 0, f关于x为奇函数,即f(-x,y)=-f(x,y) 国a咖-t. f关于x为偶函数,即f(-x,y)=f(x,y) 其中D2为D在y轴的右半部分
22 第七章 多元函数积分学 (2)若积分区域D关于y轴对称,f(x, y)为x的奇偶函数,则 ඵ 𝐷 𝑓(𝑥, 𝑦)𝑑𝜎 = 0, 𝑓关于𝑥为奇函数,即𝑓(−𝑥, 𝑦) = −𝑓(𝑥, 𝑦) 2ඵ 𝐷2 𝑓(𝑥, 𝑦)𝑑𝜎 , 𝑓关于𝑥为偶函数,即𝑓(−𝑥, 𝑦) = 𝑓(𝑥, 𝑦) 其中𝐷2为𝐷在𝑦轴的右半部分

第七章多元函数积分学 (3)若积分区域D关于原点对称,x,y)为x,y的奇偶函数,则 0, f关于x,y为奇函数,即f(-x,-y)=-f(x,y) o同2》天防得稻致ry可 其中D3为D的上半部分 (4)若积分区域D关于y=x对称,则 ro. 023
23 第七章 多元函数积分学 (3)若积分区域D关于原点对称,f(x, y)为x, y的奇偶函数,则 ඵ 𝐷 𝑓(𝑥, 𝑦)𝑑𝜎 = 0, 𝑓关于𝑥, 𝑦为奇函数,即𝑓(−𝑥, −𝑦) = −𝑓(𝑥, 𝑦) 2ඵ 𝐷3 𝑓 𝑥, 𝑦 𝑑𝜎 , 𝑓关于𝑥, 𝑦为偶函数,即𝑓(−𝑥, −𝑦) = 𝑓(𝑥, 𝑦) 其中𝐷3为𝐷的上半部分. (4)若积分区域D关于y=x对称,则 ඵ 𝐷 𝑓(𝑥, 𝑦)𝑑𝜎 = ඵ 𝐷 𝑓(𝑦, 𝑥)𝑑𝜎
第七章多元函数积分学 例4计算1=xn(y+1+y网)dxdy其中D由y=4-x名, y=一3x,x=1所围成。 4 y=4-x2 y= -3x 0 X1
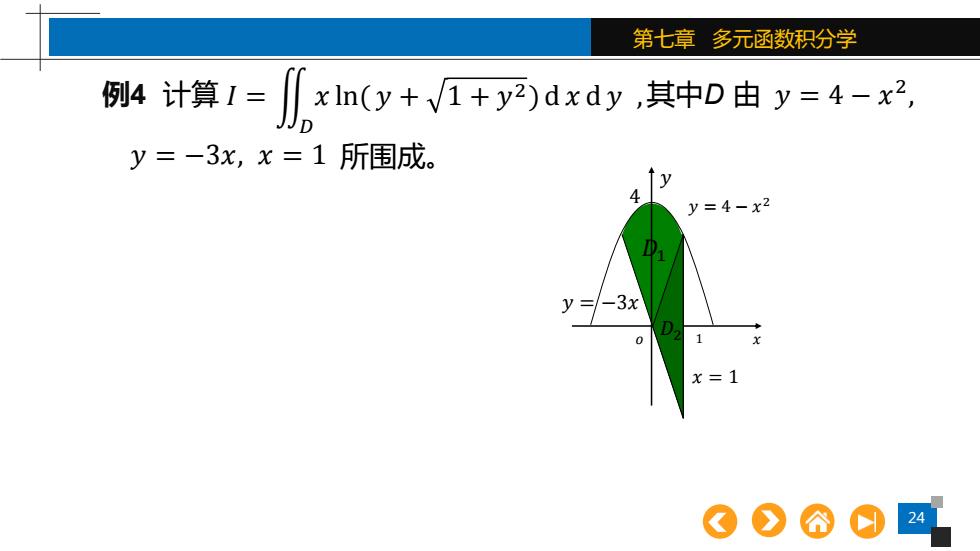
24 第七章 多元函数积分学 例4. 计算 𝐼 = ඵ 其中D 由 𝐷 𝑥 ln( 𝑦 + 1 + 𝑦 2) d 𝑥 d 𝑦 , 𝑦 = 4 − 𝑥 2 , 𝑦 = −3𝑥, 𝑥 = 1 𝑜 𝑦 1 𝑥 𝑦 = 4 − 𝑥 2 𝑦 = −3𝑥 𝐷2 𝐷1 𝑥 = 1 4 所围成

二 直角坐标系下二重积分的计算 第七章多元函数积分学 根据二重积分的定义,如果函数∫(x,y)在区域D上可积,则二重积分的值与 对积分区域的分割方法无关, △o 因此,在直角坐标系中,常用平行于x轴 和y轴的两组直线来分割积分区域D,则除 了包含边界点的一些小闭区域外,其余的小 ☑△y 闭区域都是矩形闭区域.设矩形闭区域△σ, △x 的边长为△x,和Ay,于是△o,=△x,Ay,(见 图7-7). 图7-7
25 第七章 多元函数积分学 根据二重积分的定义,如果函数 f (x, y)在区域 D 上可积,则二重积分的值与 对积分区域的分割方法无关. 二、直角坐标系下二重积分的计算 因此,在直角坐标系中,常用平行于 x 轴 和 y 轴的两组直线来分割积分区域 D ,则除 了包含边界点的一些小闭区域外,其余的小 闭区域都是矩形闭区域. 设矩形闭区域 i 的边长为 i x 和 j y ,于是 i i j = x y (见 图 7-7). O y x D i yi xi ▲▲▲ 图 7-7