
3、二重积分的性质 第七章多元函数积分学 性质4如果fcx,)=1,则有∬1dr=∬dr=D的面积; 这个性质表明:以D为底、高为1的平顶柱体的体积在数值上等于柱体的 底面积. 性质5如果在区域D上满足f(x,y)≤g(x,y),则有 ∬fx,yo≤∬gx,a; 特别地, 有 fxy)ds∬1x0
16 第七章 多元函数积分学 性质 4 如果 f x y ( , ) 1 ,则有 1d d D D x x D = = 的面积; 这个性质表明: 以 D 为底、高为 1 的平顶柱体的体积在数值上等于柱体的 底面积. 性 质 5 如果在区域 D 上满足 f x y g x y ( , ) ( , ) , 则 有 ( , )d ( , )d D D f x y g x y ; 特别地, 3、二重积分的性质 有 ( , )d | ( , ) | d . D D f x y f x y

3、二重积分的性质 第七章多元函数积分学 性质6设S,是区域D的面积.如果f(x,y)在D上有最大值M和最小值m, 则有 mSn≤∬f(x,y)do≤s。; D 这个不等式称为二重积分的估值不等式 性质7(二重积分的中值定理)如果f(x,y)在有界闭区域D上连续,则在 D上至少可以找到一点(5,),使得 ∬f(x,yo=f5,):Sn. D
17 第七章 多元函数积分学 性质 6 设 D S 是区域 D 的面积. 如果 f x y ( , )在 D 上有最大值 M 和最小值m, 则有 D D ( , d) D mS f x y MS ; 这个不等式称为二重积分的估值不等式. 性质 7 (二重积分的中值定理)如果 f x y ( , )在有界闭区域 D 上连续,则在 D 上至少可以找到一点 ( , ) ,使得 ( , )d ( , ) D D f x y f S = . 3、二重积分的性质
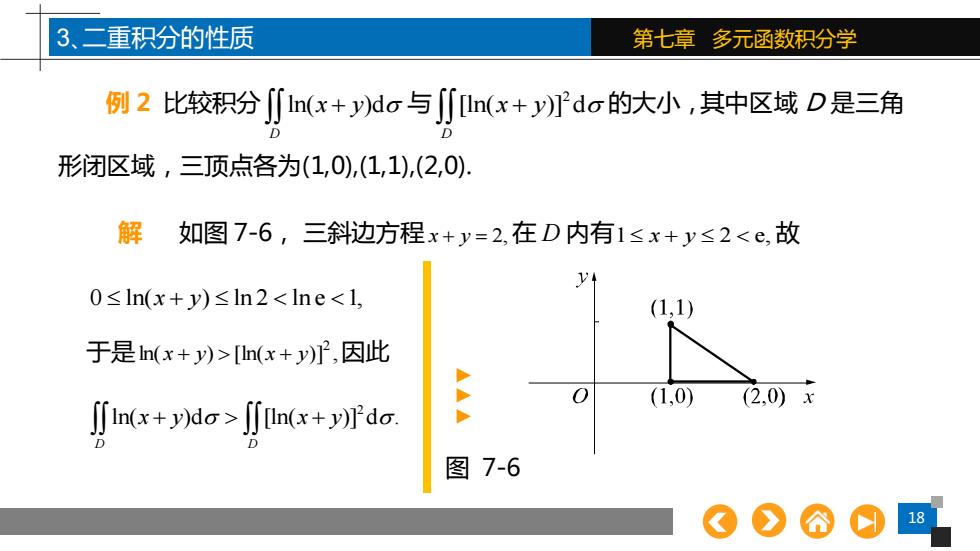
3、二重积分的性质 第七章多元函数积分学 例2比较积分ln(x+do与∬n(x+Pdo的大小,其中区域D是三角 形闭区域,三顶点各为(1,0),(1,1),(2,0): 解 如图7-6,三斜边方程x+y=2,在D内有1≤x+y≤2<e,故 0≤ln(x+y)≤ln2<lne<l, (1,1 于是n(x+y)>[n(x+y),因此 f+yd>(+do. (1,0) (2,0)x 图7-6 18
18 第七章 多元函数积分学 例 2 比较积分 ln( )d D x y + 与 2 [ln( )] d D x y + 的大小,其中区域 D 是三角 形闭区域,三顶点各为(1,0),(1,1),(2,0). 解 如图 7-6, 0 ln( ) ln 2 ln e 1, + x y 于是ln( ) [ln( )] , 2 x + y x + y 因此 2 ln( )d [ln( )] d . D D x y x y + + 3、二重积分的性质 ▲▲▲ 图 7-6 三斜边方程 x + y = 2,在 D 内有1 2 e, + x y 故

3、二重积分的性质 第七章多元函数积分学 例3不作计算,估计1=∬e+wσ的值,其中D是椭圆闭区域: x 23 (0<b<a). 解 区域D的面积o=abm,在D上因为0≤x2+y2≤a2 所以l=e°≤e+r≤e. 由性质6知o≤∬edo≤oe, 从而有abm≤∬e+yrdo≤abme. 19
19 第七章 多元函数积分学 例 3 不作计算,估计 2 2 ( ) e d x y D I + = 的值,其中 D 是椭圆闭区域: 1 2 2 2 2 + b y a x (0 b a) . 解 区域 D 的面积 = abπ, 所以 2 2 2 0 1 e e e x y a + = . 由性质 6 知 2 2 2 ( ) e d e x y a D + , 从而有 2 2 2 ( ) π e d πe x y a D ab ab + . 3、二重积分的性质 在 D 上因为0 , 2 2 2 x + y a

第七章多元函数积分学 性质8二重积分的对称性定理 (I)若积分区域D关于x轴对称,化,)为y的奇偶函数,则 0 f关于y为奇函数,即f(x,-y)=-f(x,y) do 2n,fx)do,f关于为偶函数,即fx,-)=fx,y) 其中D,为D在x轴的上半部分
20 第七章 多元函数积分学 性质8 二重积分的对称性定理 (1)若积分区域D关于x轴对称,f(x, y)为y的奇偶函数,则 �� 𝑓(𝑥,𝑦)𝑑𝜎 = 0, 𝑓关于𝑦为奇函数,即𝑓(𝑥, −𝑦) = −𝑓(𝑥,𝑦) 2 ��1 𝑓(𝑥,𝑦)𝑑𝜎 , 𝑓关于𝑦为偶函数,即𝑓(𝑥, −𝑦) = 𝑓(𝑥, 𝑦) 其中𝐷1为𝐷在𝑥轴的上半部分