
直角坐标系下二重积分的计算 第七章多元函数积分学 故在直角坐标系中,面积微元do可记为dxdy,即do=dxdy.进而把二 重积分记为川f(x,y)dxdy,这里我们把dxdy称为直角坐标系下的面积微元. 在实际应用中,直接通过二重积分的定义和性质来计算二重积分一般是困难 的,本节和下一节,我们要讨论二重积分的计算方法,其基本思想是将二重积分 化为两次定积分来计算,转化后的这种两次定积分常称为二次积分或累次积分 本节先在直角坐标系下讨论二重积分的计算
26 第七章 多元函数积分学 在实际应用中,直接通过二重积分的定义和性质来计算二重积分一般是困难 的, 二、直角坐标系下二重积分的计算 故在直角坐标系中,面积微元d 可记为 d dx y , 即d d d = x y . 进而把二 重积分记为 ( , )d d D f x y x y ,这里我们把d dx y 称为直角坐标系下的面积微元. 本节先在直角坐标系下讨论二重积分的计算. 本节和下一节,我们要讨论二重积分的计算方法,其基本思想是将二重积分 化为两次定积分来计算,转化后的这种两次定积分常称为二次积分或累次积分

1、矩形区域上的二重积分 第七章多元函数积分学 设函数z=f(x,y)在矩形区域 D={(x,y)川a≤x≤b,c≤y≤d上连续, 且f(x,y)≥0. 由前面的内容可知,fx,y)dxdy的值等于以D为底,以曲面z=fx,y)为 D 顶的曲顶柱体的体积
27 第七章 多元函数积分学 设函数 z f x y = ( , )在矩形区域 D x y a x b c y d = {( , ) | , }上连续, 且 f x y ( , ) 0 . 由前面的内容可知, ( , )d d D f x y x y 的值等于以 D 为底,以曲面 z f x y = ( , )为 顶的曲顶柱体的体积. 1、矩形区域上的二重积分
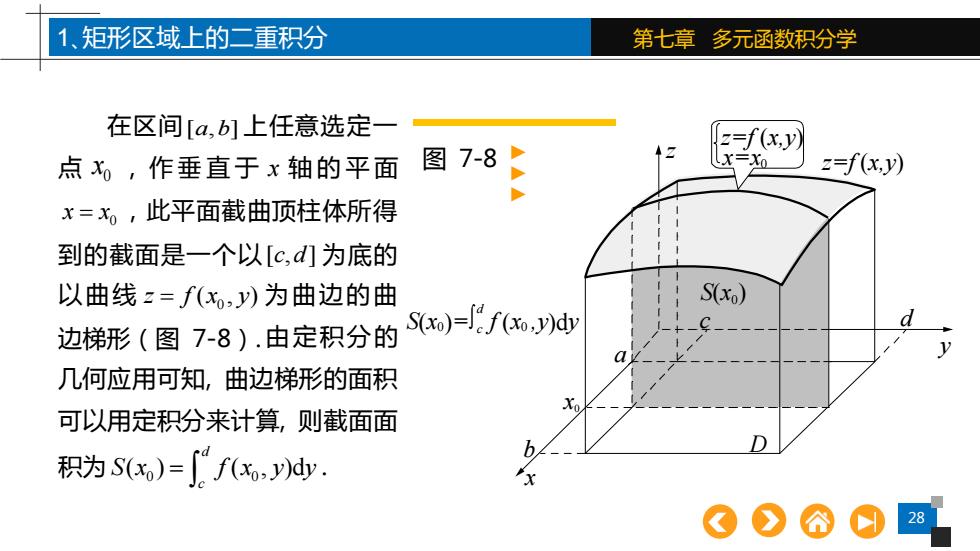
1、矩形区域上的二重积分 第七章多元函数积分学 在区间[a,b]上任意选定一 z=f(x,y) 点x,作垂直于x轴的平面 图7-8♪ x=Xo z=f(x.y) x=x。,此平面截曲顶柱体所得 到的截面是一个以[c,d]为底的 以曲线z=f(x,y)为曲边的曲 S(xo) Sxo)=fo,yd d 边梯形(图7-8).由定积分的 几何应用可知,曲边梯形的面积 可以用定积分来计算,则截面面 积为S(x)=fo,dy. b
28 第七章 多元函数积分学 在区间 [ , ] a b 上任意选定一 点 0 x ,作垂直于 x 轴的平面 0 x x = ,此平面截曲顶柱体所得 到的截面是一个以[ , ] c d 为底的 以曲线 0 z f x y = ( , ) 为曲边的曲 边梯形(图 7-8). 1、矩形区域上的二重积分 c S(x0) D d a z=f (x,y) S(x0)= d c f (x0 ,y)dy y x z z=f (x,y) x=x0 x0 由定积分的 几何应用可知, 曲边梯形的面积 可以用定积分来计算, 则截面面 积为 0 0 ( ) ( , )d d c S x f x y y = . 图 7-8 b▲▲▲

1、矩形区域上的二重积分 第七章多元函数积分学 对于区间[a,b]上的任何一点x,对应的截面面积为 Sx)=∫fx,. 故曲顶柱体的体积V为 r-sxwr=Lfx-广dft 即 ∬fx,yhd=dffx, (1) 式(1)的右端称为先对y后对x的二次积分. 这个公式表明,矩形区域上的二重积分可以转化为先对y后对x的二次积分 来计算
29 第七章 多元函数积分学 对于区间[ , ] a b 上的任何一点 x,对应的截面面积为 ( ) ( , )d d c S x f x y y = . 故曲顶柱体的体积V 为 ( )d ( , )d d d ( , )d b b d b d a a c a c V S x x f x y y x x f x y y = = = 即 ( , )d d d ( , )d b d a c D f x y x y x f x y y = . (1) 式(1)的右端称为先对 y 后对x 的二次积分. 这个公式表明,矩形区域上的二重积分可以转化为先对 y 后对x的二次积分 来计算. 1、矩形区域上的二重积分

1、矩形区域上的二重积分 第七章多元函数积分学 例1计算定积分∫(x+yy 解 因为被积函数x+y是x,y的二元函数,而积分变量是y.因此求x+y 的原函数的时候,可以把x看成是常数,故原函数为x·y+y 故定积分的值为 +t=+]5=0-0+02-0的=x+ 2x+1 22 这是一个关于x的函数: 0
30 第七章 多元函数积分学 例 1 计算定积分 1 0 ( )d x y y + . 解 因为被积函数 x y + 是 x y, 的二元函数,而积分变量是 y . 故定积分的值为 1 0 ( )d x y y + 这是一个关于 x的函数. 1、矩形区域上的二重积分 1 2 1 0 0 1 = | | 2 x y y + = 1 2 2 (1 0) (1 0 ) 2 x − + − 1 2 1 2 2 x x + = + = . 因此求 x y + 的原函数的时候,可以把 x看成是常数,故原函数为 1 2 2 x y y +