
引理4.3.1.(步长的存在性).假设f∈C1,p)是()处的下降方向,且f沿着射线{x()+ ap):a>0}有下界.如果1>g>p>0,则满足Wole条件和强Wole条件的可接受区间存 在. 证明因为a)=f(()+ap)对所有a>0有下界,且0<p<1,所以p-线(a)= f+apg'p)与(a)的图形至少相交一次.设ad是最小的交点,即d=min{a>0: l(a)=(a)}.由ad的选取可知 f侧+ap例=5肉+p()p(倒, (4.3.7) 且区间(0,a)中的任一a都满足(4.3.1).再由中值定理,存在a”∈(0,a)满足 f(ax(肉+dp)-f=adg(+a”p)Tp. (4.3.8) 由(4.3.7)和(4.3.8)有 ge侧+a'p网)Tp倒=Pg侧Tp因>gTp, (4.3.9) 最后一个不等式是因为p<g且g(倒Tp侧<0.因此a满足Wole条件,且其中的不等式是 严格成立的.因此,由f的光滑性假设,存在包含a”的区间,Wolfe条件在该区间上成立.此 外,因为(4.3.9)的左端是负的,所以强Wole条件在相同的区间上成立
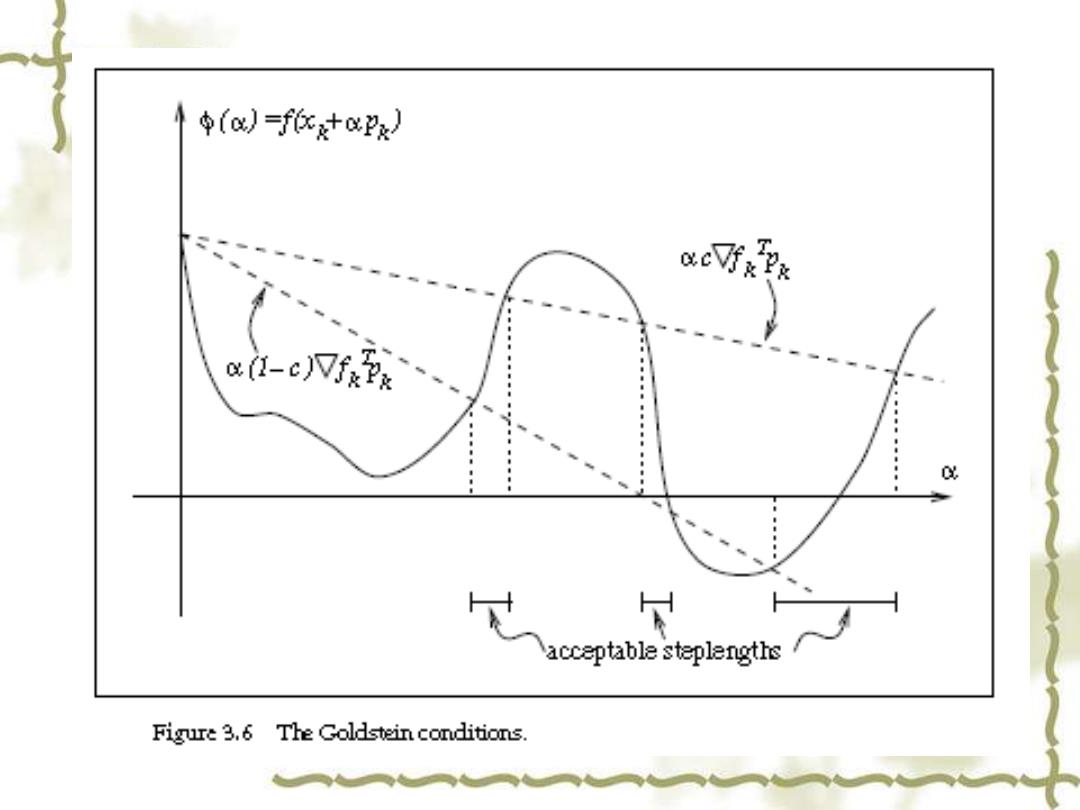
中()=f在+xJ e听安 x江-c)贝f 0 acceptable steplengths Figure 3.6 The Goldstein conditions

0()=fx+0Pk) Nolfe条件: line of sufficient decrease 1o) (a)≤(0)+apt(0) desired slope 0 中(a)≥g(0),g∈(p,1) acceptable acceptable 1(a)川≤-o(0) Figure 3.5 Step lengths satisfying the Wolfe conditions. 实践中,σ=0.9相当于很弱(限制性不强)的线搜索,而σ=0.1则对应相当精确的线搜 索.σ值越小,满足条件的步长区间越短,线搜索时间越长.因此,除了检验精确线搜索的理 论假设外,通常很少使用小的σ值.当搜索方向p冈由牛顿法或拟牛顿法选定时,σ的典型 值是0.9当p)由非线性共轭梯度法获得时,σ的典型值是0.1.至于p,典型值是10-4.最后, 需要指出的是,Goldstein的另一个条件(4.3.1),也称为Armijo条件,它有可能让可接受区间位 于真正极小点的左侧.但实践中这种情祝几乎不会出现,而且它的优点是排除了α=∞这 种麻烦情况
Wolfe条件:

(四)收敛性分析 定理4.1设目标函数fw)一阶可微,且水平集G,={xf(x)≤fx)} 有界,则最速下降法或者在有限步迭代后终止;或者得到点列x}, 它的任何极限点都是fx)的驻点。 证明:见p68定理4.1的证明. 推论4.1如果函数fx)为凸函数,则应用最速下降法,或者在有限步 迭代后终止;或者得到点列{x“,的任何极限点都是全局极小点。 证明:见课本P69推论4.2 下面讨论最速下降法用于二次函数时的收敛性分析
(四) 收敛性分析 定理4.1 设目标函数f (x)一阶可微,且水平集 有界,则最速下降法或者在有限步迭代后终止;或者得到点列 , 它的任何极限点都是f (x)的驻点。 0 0 G x f x f x = ( ) ( ) { }k x 证明:见p68定理4.1的证明. 推论4.1 如果函数f (x)为凸函数,则应用最速下降法,或者在有限步 迭代后终止;或者得到点列 的任何极限点都是全局极小点。 下面讨论最速下降法用于二次函数时的收敛性分析。 { }k x 证明:见课本P69推论4.2

用于二次函数时的收敛性分析 定理4.3:对于二次函数f(x)=2x2x,2为对称正交,九,九分别 为其最小最大特征值,从任意初点,出发,对此二次函数,用最速下降 法产生的序列x},对于k≥0有 ×无法显示该图片。 2.二fx) f元.+元 并且 川x川 由于 =1 -<1,则x4→0 n+九 而函数f(x)=)x'Ox的极小点恰好是x=0。故最速下降法对于 二次函数关于任意初点均收敛,而且是线性收敛的
用于二次函数时的收敛性分析 1 1 1 n n q − = + 并且 1 2 1 1 ( ) ( ) ( ) n k k n f x f x + − + 1 0 1 1 || || || || k n n k n x x − + 0 x { }k x k 0 定理4.3:对于二次函数 Q为对称正交, 分别 为其最小最大特征值,从任意初点 出发,对此二次函数,用最速下降 法产生的序列 ,对于 有 1 2 ( ) , T f x x Qx = 1 n , 由于 ,则 xk → 0 而函数 的极小点恰好是 。故最速下降法对于 二次函数关于任意初点均收敛,而且是线性收敛的。 1 ( ) 2 T f x x Qx = * x = 0