
为了清除最优步长最速下降法中两个搜索方向正交的不良后果,人们发 现了不少方法,如: ()选择不同初始点 例:问题: min f(x)=x2+25x2 取初点 x,=(2,2)'f(x)=104,f(x)=(4,100) 为求七,沿-7fx)方向从x出发求f(x)的极小点 即进行线搜索 minf(x-avf(x)) min(2-4)'+25(2-1002)Amin(2) 1>0 则 p(2)=-8(2-42)-5000(2-1002)=0 626 解得 ≈0.02003072 31252
2 2 min ( ) 25 1 2 f x x x = + ( ) 0 2,2 T x = ( ) ( ) ( ) 0 0 104, 4,100 T f x f x = = 1 x ( ) 0 − f x 0 x f x( ) ( 0 0 ( )) 0 min f x f x − ( ) ( ) 2 2 0 min{ 2 4 25 2 100 } min ( ) − + − ' ( ) 8(2 4 ) 5000(2 100 ) 0 = − − − − = 0 626 0.02003072 31252 = 为了清除最优步长最速下降法中两个搜索方向正交的不良后果,人们发 现了不少方法,如: (1) 选择不同初始点 例:问题: 取初点 为求 ,沿 方向从 出发求 的极小点 即进行线搜索 则 解得

y=-f(x,)=(1.919877-0.3071785×102)1 f(x1)=3.686164. 然后再从x开始新的迭代,经过10次迭代,得最优解x=(0,0)/计算中可 以发现,开始几次迭代,步长比较大,函数值下将降较快但当接进最优点 时,步长很小,目标函数值下降很慢。如果不取初点为x,=(2,2)丫而取 x=(100,月虽然后一初点较前一初点离最优点x=(0,0)了远,但迭代中 不会出现上面的锯齿现象。这时: f(x)=(2x0,50x)=(20,0) p(2)[400-2002}+25(0-02]=400(100-202) 九=i,x=-f(x)=(0,0) 一步就得到了极小点
( ) ( ) 2 1 0 0 0 1.919877 0.3071785 10 T x x f x − = − = − 1 f x( ) 3.686164. = 然后再从 开始新的迭代,经过10次迭代,得最优解 计算中可 以发现,开始几次迭代,步长比较大,函数值下将降较快但当接进最优点 时,步长很小,目标函数值下降很慢。如果不取初点为 而取 1 x * (0,0)T x = 0 (2, 2)T x = 0 (100,0)T x = * (0,0)T x = ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 0 0 0 1 2 2 2 0 1 0 0 0 2 ,50 200,0 100 200 25 0 0 400 100 200 1 , 0,0 2 T T f x x x d d x x f x = = = − + − = − − = = − = 一步就得到了极小点。 虽然后一初点较前一初点离最优点 远,但迭代中 不会出现上面的锯齿现象。这时:

可见:造成距齿现象与初始点的选择有关,但怎样选一个初始点也是一 件困难的事。 (2)采用不精确的一维搜索:用一维搜索求出的步长为入时,我们不 取九,=入,而用入的一个近似值作为2,这样可使相邻两个迭代点处的 梯度不正交,从而改变收敛性。 对于最速下降法,有时为了减少计算工作量,不采用直线搜索确定步长, 而采用固定步长的方法,称为固定步长最速下降法。只要充分小,总有: -小水-8, 但到底取多大,没有统一的标准,取小了,收敛太慢,而取大了, 又会漏掉极小点。—不精确线搜索解决这个问题
( ) ( ) ( ) ( ) 1 k k k k k f x f x f x f x f x + = − (2)采用不精确的一维搜索:用一维搜索求出的步长为 时,我们不 取 ,而用 的一个近似值作为 , 这样可使相邻两个迭代点处的 梯度不正交,从而改变收敛性。 可见:造成距齿现象与初始点的选择有关,但怎样选一个初始点也是一 件困难的事。 * k = * k 对于最速下降法,有时为了减少计算工作量,不采用直线搜索确定步长, 而采用固定步长λ的方法,称为固定步长最速下降法。只要λ充分小,总有: 但λ到底取多大,没有统一的标准, λ取小了,收敛太慢,而λ取大了, 又会漏掉极小点。——不精确线搜索解决这个问题 *

中侧=f在+哩x} c阅 acceptable acceptable
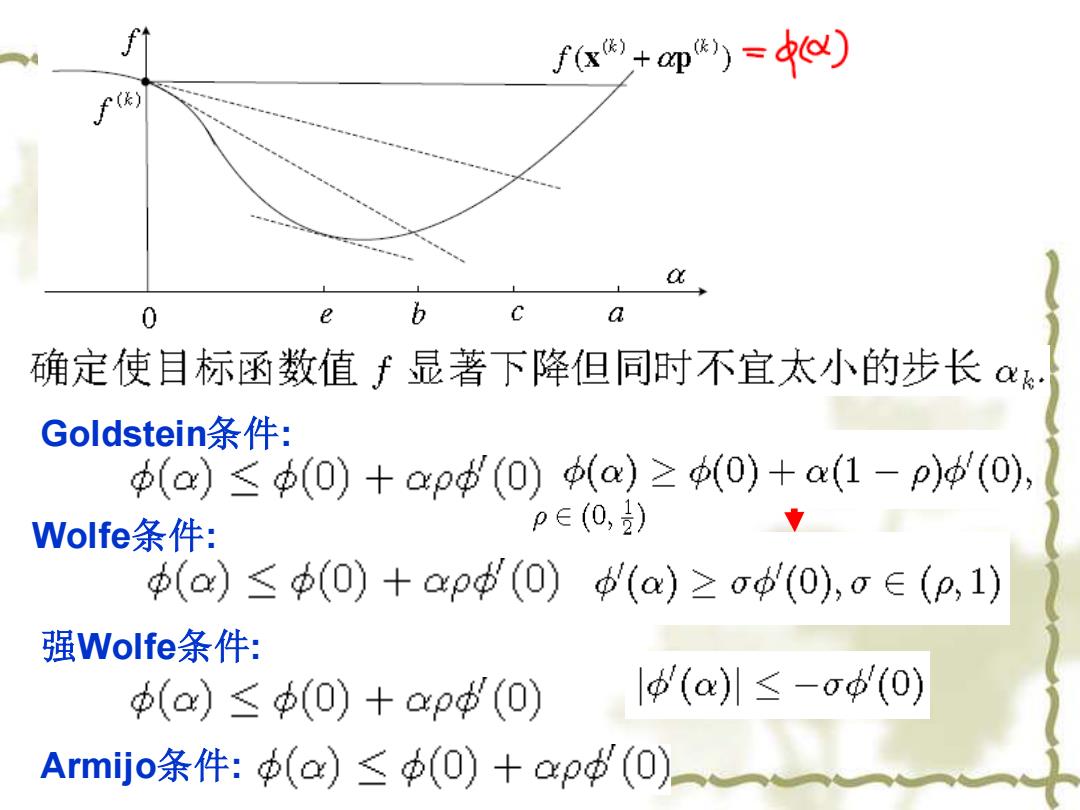
f(x+ap)=) 0 b C a 确定使目标函数值f显著下降但同时不宜太小的步长· Goldstein条件: (a)≤(0)+ap(0)(a)≥0)+a(1-p)p'(0), Nolfe条件: p∈(0,) 中(a)≤(0)+ap(O)(a)≥o(0),o∈(p,1) 强Wolfe条件: (a)≤(0)+ap(0) 1p()川≤-o'(0) Armijo条件:(a)≤(O)+apt(O)
Goldstein条件: Wolfe条件: 强Wolfe条件: Armijo条件: