微分方程模型 0、简例 1、人口预报问题 2、传染病问题 3、作战模型 4、捕食问题 5、火箭发射问题 6、药物吸收、真假绘画作品鉴定、 交通管理/堵塞问题 ■■
微分方程模型 1、人口预报问题 3、作战模型 4、捕食问题 5、火箭发射问题 ……… 2、传染病问题 6、药物吸收、真假绘画作品鉴定、 交通管理/堵塞问题 0、简例
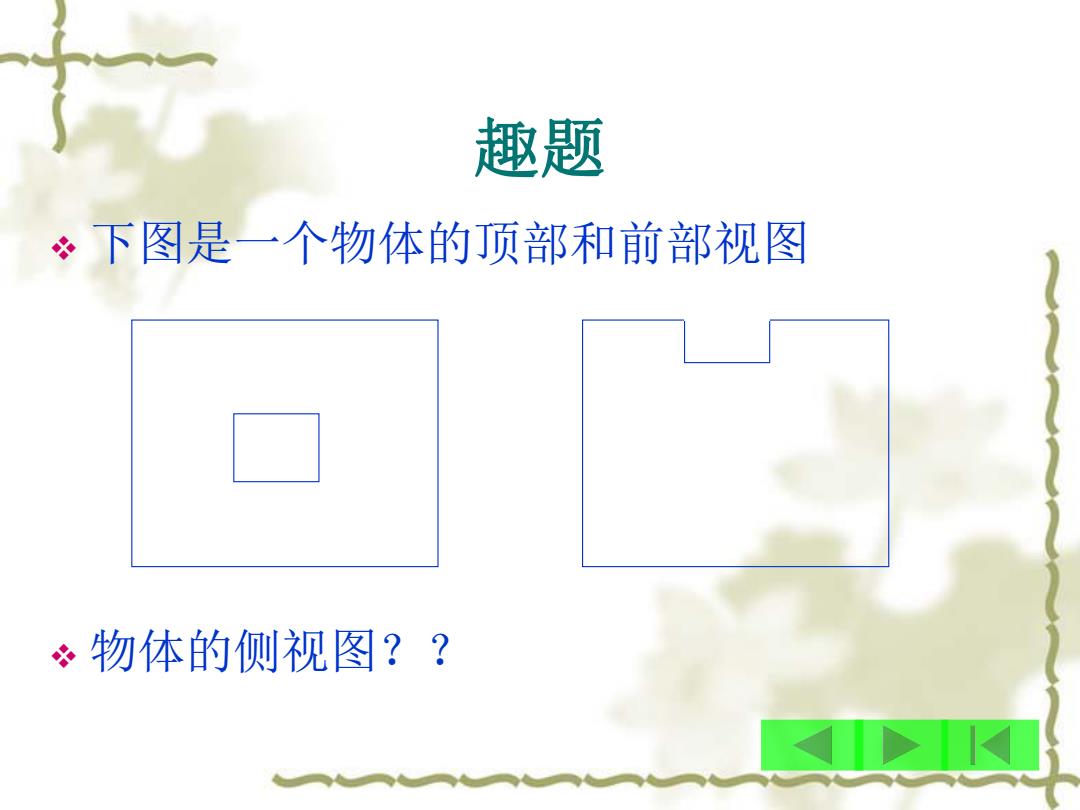
趣题 ·下图是一个物体的顶部和前部视图 。物体的侧视图??
趣题 v 下图是一个物体的顶部和前部视图 v 物体的侧视图??
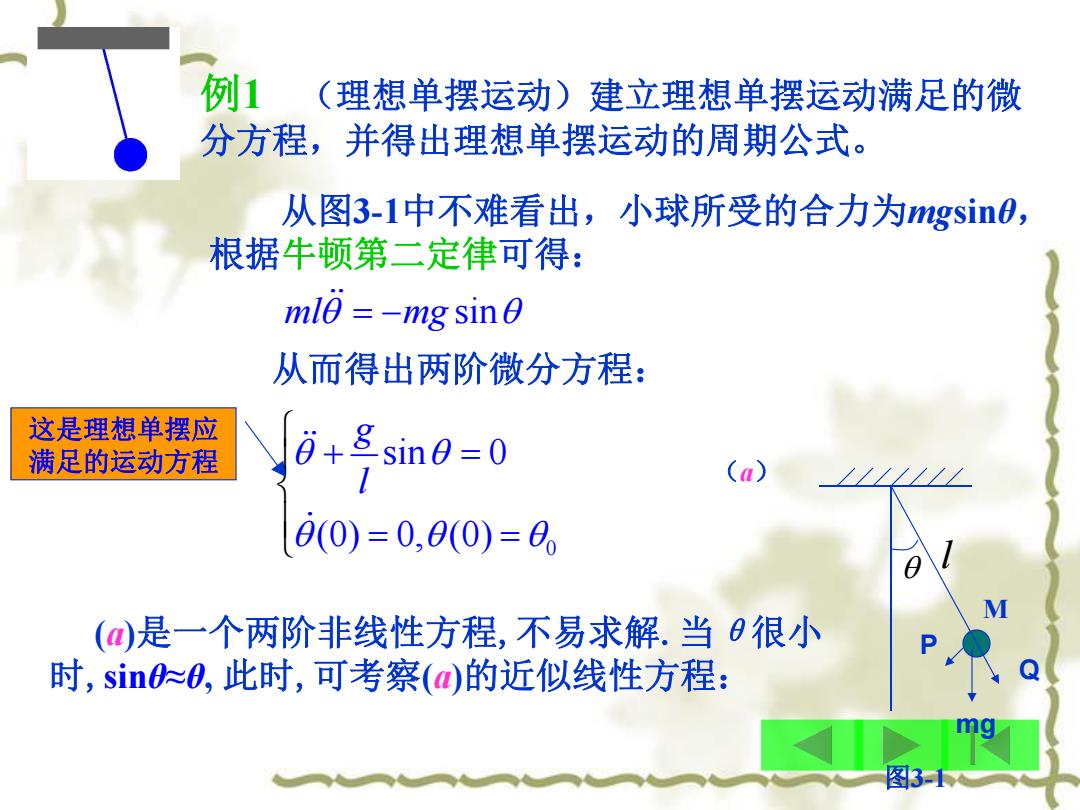
例1 (理想单摆运动)建立理想单摆运动满足的微 分方程,并得出理想单摆运动的周期公式。 从图3-1中不难看出,小球所受的合力为ngsin0, 根据牛顿第二定律可得: mle =-mg sin 从而得出两阶微分方程: 这是理想单摆应 满足的运动方程 6+sin0=0 a) 0(0)=0,0(0)=0 (是一个两阶非线性方程,不易求解,当0很小 时,sin~0,此时,可考察(的近似线性方程: g
例1 (理想单摆运动)建立理想单摆运动满足的微 分方程,并得出理想单摆运动的周期公式。 从图3-1中不难看出,小球所受的合力为mgsinθ, 根据牛顿第二定律可得: ml mg sin 从而得出两阶微分方程: 0 sin 0 (0) 0, (0) g l (a) 这是理想单摆应 满足的运动方程 (a)是一个两阶非线性方程,不易求解.当θ很小 时,sinθ≈θ, 此时,可考察(a)的近似线性方程: M Q P mg l 图3-1
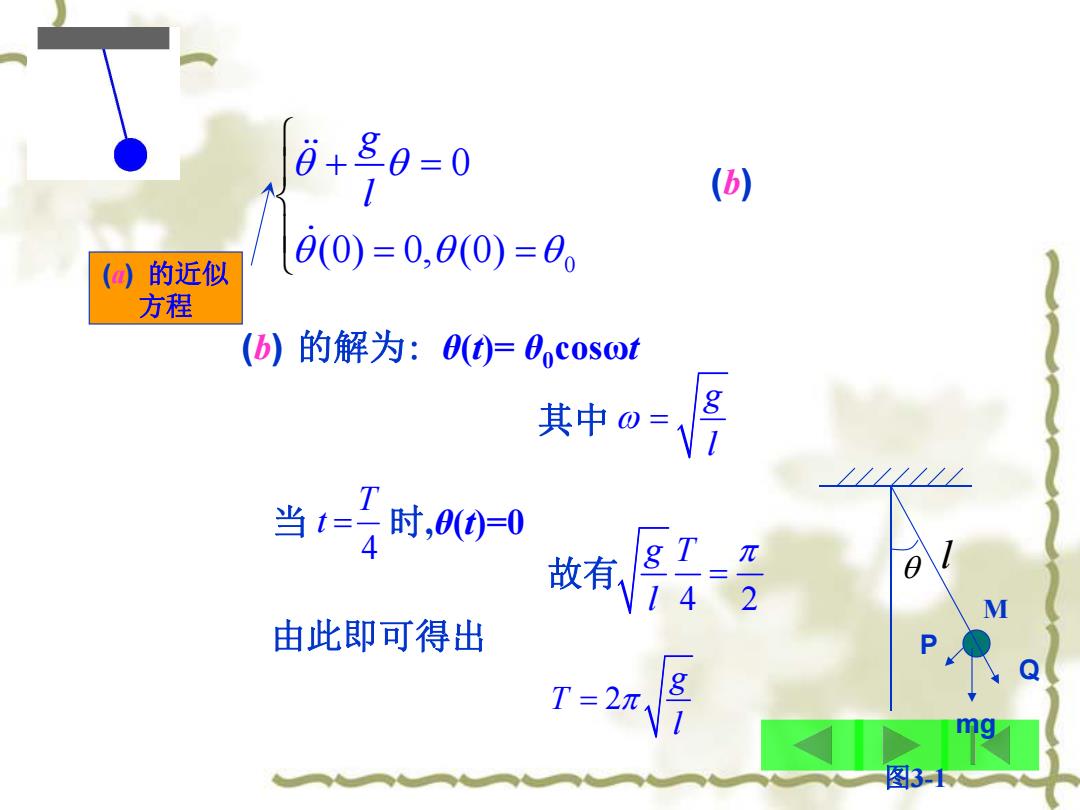
6+80=0 () ()的近似 0(0)=0,0(0)=8 方程 (b)的解为:0()=0ocos@t 其中o三的 当1=乙时,0c-0 4 故有、 T 2 14 由此即可得出 g T=2π mg 图31
0 0 (0) 0, (0) g l (b) 由此即可得出 2 g T l (b) 的解为: θ(t)= θ0cosωt g l 其中 当 时,θ(t)=0 4 T t 4 2 g T l 故有 M Q P mg l 图3-1 (a) 的近似 方程

例2市场价格模型 对于纯粹的市场经济来说,商品市场价格取决于市场供需之 间的关系,市场价格能促使商品的供给与需求相等(这样的价格 称为(静态)均衡价格)也就是说,如果不考虑商品价格形成的动 态过程,那么商品的市场价格应能保证市场的供需平衡,但是,实 际的市场价格不会恰好等于均衡价格,而且价格也不会是静态的, 应是随时间不断变化的动态过程.建立描述市场价格形成的动 态过程的数学模型。 假设在某一时刻t,商品的价格为p(),它与该商品的均衡价 格间有差别,此时,存在供需差,此供需差促使价格变动.对新的 价格,又有新的供需差,如此不断调节,就构成市场价格形成的 动态过程,假设价格p()的变化率dp/dt与需求和供给之差成正 比,并记fp)为需求函数,gp)为供给函数,于是 =k[f(p-g(p] dt
例2 市场价格模型 对于纯粹的市场经济来说,商品市场价格取决于市场供需之 间的关系,市场价格能促使商品的供给与需求相等(这样的价格 称为(静态)均衡价格).也就是说,如果不考虑商品价格形成的动 态过程,那么商品的市场价格应能保证市场的供需平衡,但是,实 际的市场价格不会恰好等于均衡价格,而且价格也不会是静态的, 应是随时间不断变化的动态过程. 建立描述市场价格形成的动 态过程的数学模型。 d d p k f p g p t 假设在某一时刻 t, 商品的价格为 p(t), 它与该商品的均衡价 格间有差别, 此时, 存在供需差, 此供需差促使价格变动. 对新的 价格, 又有新的供需差, 如此不断调节, 就构成市场价格形成的 动态过程, 假设价格p(t)的变化率dp/dt 与需求和供给之差成正 比, 并记 f(p) 为需求函数, g(p) 为供给函数, 于是