
第3讲 凸集、凸函数、 凸规划 凸性(Convexity)是最优化理论必须涉及到基本概念.具有凸性 的非线性规划模型是一类特殊的重要模型,它在最优化的理 论证明及算法研究中具有非常重要的作用. 凸集(Convex Set) 凸函数(Convex Function) 凸规划(Convex Programming)
第3讲 凸集、凸函数、凸规划 • 凸集 (Convex Set) • 凸函数 (Convex Function) • 凸规划 (Convex Programming) 凸性(Convexity)是最优化理论必须涉及到基本概念.具有凸性 的非线性规划模型是一类特殊的重要模型,它在最优化的理 论证明及算法研究中具有非常重要的作用

凸集定义 线性组合linear Combination ∑x,其中儿,∈R,x,∈R”,i=1,2,…m. i=1 仿射组合(Affine Combination) 2x其申cRxER',i=12m且23,=1 i=1 凸组合(Convex Combination) 之x,其中,eR*,y,eR",i=1,2m且∑=1. i=1 凸锥组合(Convex Cone Combination) ∑,其中2eR*,x,eR”,i=1,2m
凸集---定义 , , , 1,2,... , 1. 1 1 = = = = m i i n i i m i i xi 其 中 R x R i m 且 , , , 1,2,... . 1 x R x R i m n i i m i i i = + = 其 中 线性组合 (linear Combination) , , , 1,2,... . 1 x R x R i m n i i m i i i = = 其 中 仿射组合 (Affine Combination) , , , 1,2,... 1. m i 1 i 1 = + = x 其 中 R x R i = m且 = n i i m i i i 凸组合 (Convex Combination) 凸锥组合 (Convex Cone Combination)

凸集-定义 例二维情况下,两点xx2的 (a)线性组合为全平面 (b)仿射组合为过这两点的直线: (c)凸组合为连接这两点的线段 (b)凸锥组合为以原点为锥顶并通过这两点的锥
凸集---定义 例 二维情况下,两点x1 , x2 的 (a)线性组合为全平面; (b)仿射组合为过这两点的直线; (c)凸组合为连接这两点的线段; (b)凸锥组合为以原点为锥顶并通过这两点的锥
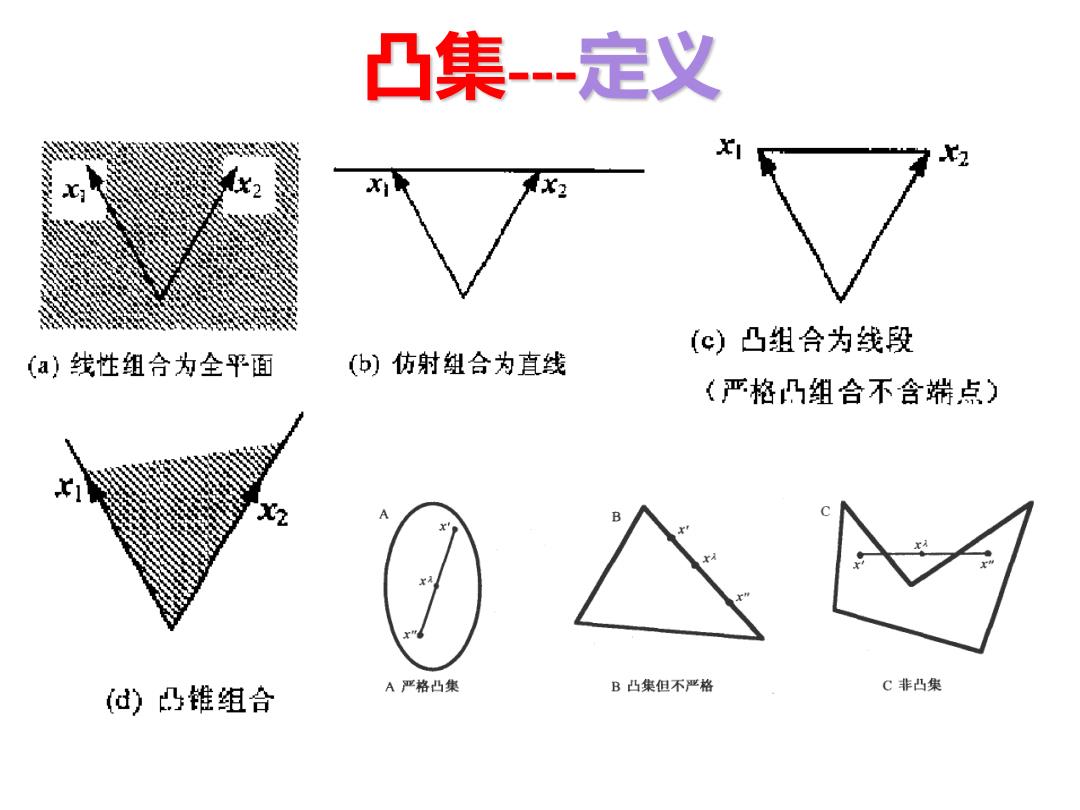
凸集--定义 XI 2 X2 (c)凸组合为线段 (a)线性组合为全平面 (b)仿射組合为直线 (严格凸组合不含端点) (d)凸锥组合 A严格凸集 B凸集但不严格 C非凸集
凸集---定义

凸集-定义 定义1i 设集合DcR”,若对于任意两点 x,y∈D,及实数az(0≤a≤1),都有: ax+1-a)y∈D, 则称集合D为凸集 常见的凸集:单点集{x},空集☑,整个欧氏空间R”, 超平面H={x∈R”l4x1+ax2++anxn=b以 半空间: H*={x∈R"lax+ax2++anxn≥b} -xER"a"x=b
凸集---定义 定义1 设集合 , n D R 若对于任意两点 x , y D, 及实数 (0 1), 都有: x + (1−)y D, 则称集合 D 为凸集. 常见的凸集:单点集 { x },空集 ,整个欧氏空间 Rn , 超平面: , H x R a1 x1 a2 x2 an xn b n = + ++ = 半空间: 1 1 2 2 = n n n n T H x R a x a x a x b x R a x b + = + + +