
4.无约束规划 无约束规划建模—引例 无约束规划模型 无约束规划的示意图 无约束规划的性质 无约束规划重要算法 2 用MATLAB解无约束规划
4. 无约束规划 无约束规划建模——引例 无约束规划模型 无约束规划的示意图 无约束规划的性质 无约束规划重要算法 用MATLAB解无约束规划

“定位问题”一厂址选择等 引例1: 某城市要选定一个供应中心(供电、供水、公天然气、 网络接入等)的位置,该中心向城市中由固定位置的个用户提 供服务。问如何确定这个中心的位置才是最合理的? 解设用户位置为(4,b=1,2,m已知,而供应中心的位置 是(c,x2);假设运输线路不受道路影响,只考虑直线距离,则 可建立求总距离最短的数学模型为: min f(x,x2)=∑2V(x,-a}+(2-,月 若进一步考虑各单位的用量w,不同,而运价c按距离 计算,则可建立求总总费用最小的数学模型为: mimf(x,x2)=c∑0w,V(c,-a}+(2-b,月 其中:c—运价(元/吨公里);w,—第个用户的需求量
引例1: 某城市要选定一个供应中心(供电、供水、公天然气、 网络接入等)的位置,该中心向城市中由固定位置的m个用户提 供服务。问如何确定这个中心的位置才是最合理的? 解 设用户位置为(ai , bi )(i=1,2,...,m)已知,而供应中心的位置 是(x1 , x2 );假设运输线路不受道路影响,只考虑直线距离,则 可建立求总距离最短的数学模型为: ( ) ( ) = = − + − m i x x x ai x bi f 1 2 2 2 1 2 1 min ( , ) 其中:c——运价(元/吨公里);wi——第i个用户的需求量. ( ) ( ) = = − + − m i wi x ai x bi f x x c 1 2 2 2 1 2 1 min ( , ) 若进一步考虑各单位的用量wi不同,而运价c按距离 计算,则可建立求总总费用最小的数学模型为: “定位问题”——厂址选择等

“最小二乘问题”一解方程组 引例2:在某些实际问题中,往往要求决策变量x1,x2,,xn满 足(或近似满足)某些平衡条件,它表现为要求x1,X2,,xn满足 方程组 f(x1,…,xn)=03j=1,2,…,p 可转化为求解问题: min 2G,,x,月 即要求均方误差最小—最小二乘问题,包括线性最小 二乘和非线性最小二乘问题,在数学建模中有非常重要的应 用
引例2:在某些实际问题中,往往要求决策变量x1 , x2 , ..., xn满 足(或近似满足)某些平衡条件,它表现为要求x1 , x2 , ..., xn满足 方程组 fj (x1 , , xn ) = 0, j = 1,2, , p 即要求均方误差最小——最小二乘问题,包括线性最小 二乘和非线性最小二乘问题,在数学建模中有非常重要的应 用。 ( ) = m j x xn f 1 2 1 min ( ,, ) 可转化为求解问题: “最小二乘问题”——解方程组
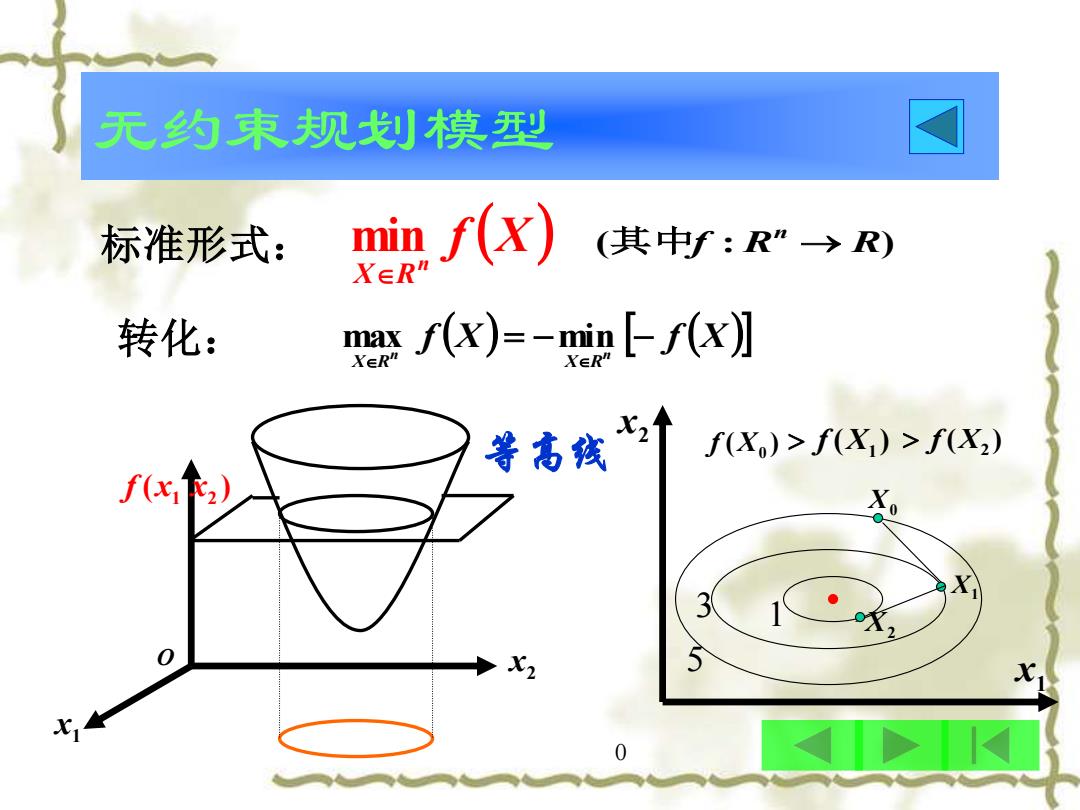
无约束规划模型 标准形式: ip(x) (其中f:R”>R) 转化: axf(x)=-in上f(x】 等高孩 f(X)>f(X)>f(X2) f(x) 3 0 X2 0
无约束规划模型 标准形式: f (X ) n XR min ( f : R R) 其中 n → f (X) f (X) n n X R X R = − − 转化: max min 等高线 1 x 2 x ( ) x1 x2 f O 1 x 2 x 0 5 3 1 X0 X1 X2 ( ) X0 f ( ) X1 f ( ) X2 f
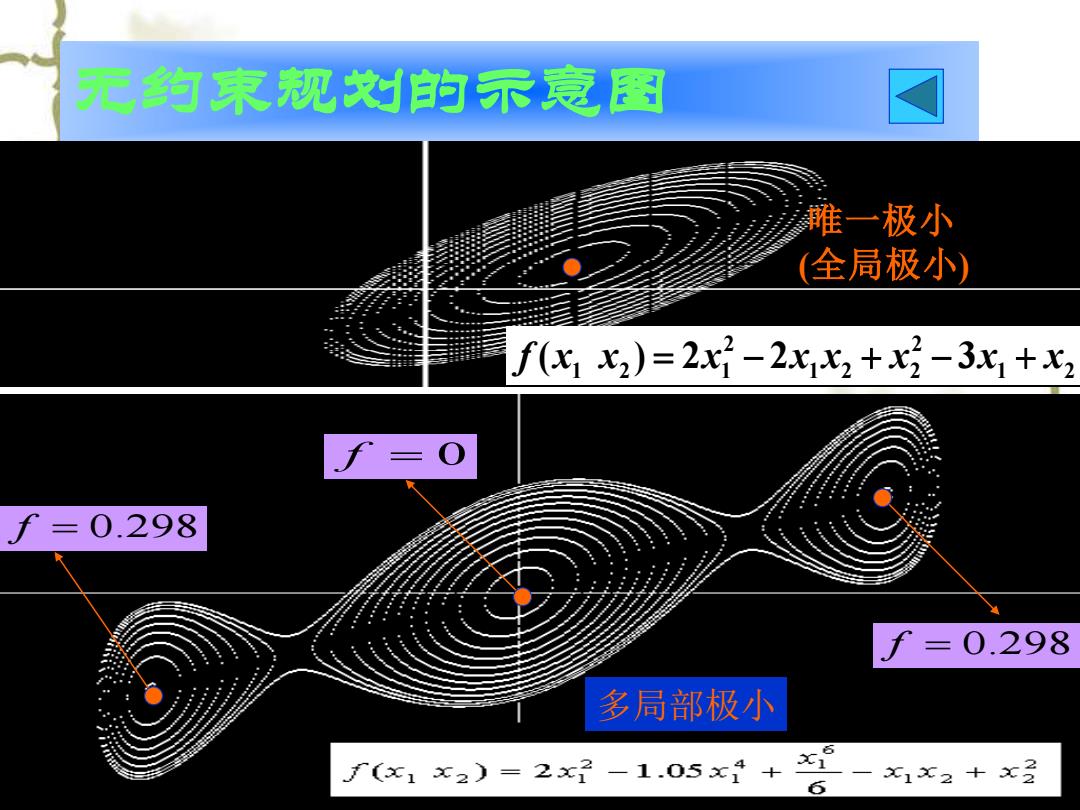
无约束视对的示意,图 睢一极小 全局极小) f(K1x2)=2x2-2x2+-3x1+x2 f=0.298 f=0.298 多局部极小 f(x1x2)=2x7-1.05x4 31 x1x2+x经 6
无约束规划的示意图 多局部极小 f = 0.298 f = 0 f = 0.298 唯一极小 (全局极小) 1 2 2 1 2 2 2 1 2 1 f (x x ) = 2x − 2x x + x − 3x + x