
运输问题 运输问题的表示 网络图、线性规划模型、运输表 区初始基础可行解 西北角法、最小元素法 求解方法 闭回路法、对偶变量法 ● 特殊形式运输问题 不平衡问题、转运问题
运输问题 运输问题的表示 网络图、线性规划模型、运输表 初始基础可行解 西北角法、最小元素法 求解方法 闭回路法、对偶变量法 特殊形式运输问题 不平衡问题、转运问题
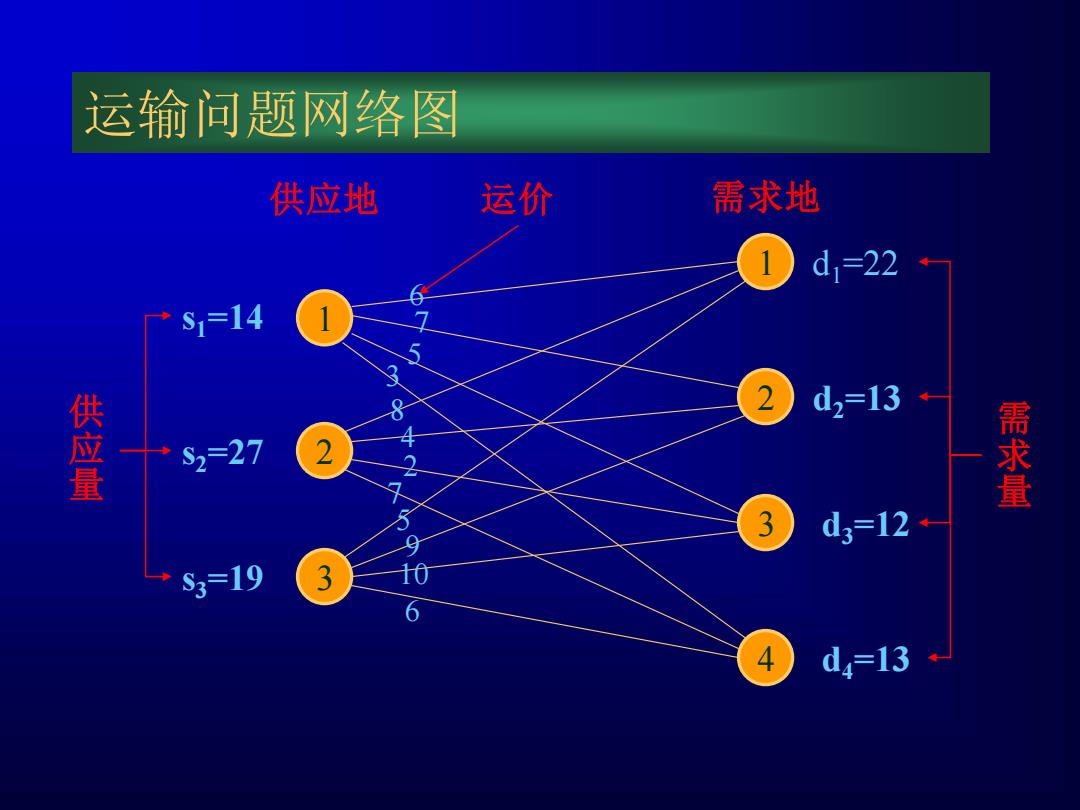
运输问题网络图 供应地 运价 需求地 d1=22 S1=14 67 5 2 d2-13 供应量 S2=27 2 S3=19 3 8+28步06 需求量 3 d3=12 4 d4=13
23 2 1 341 运输问题网络图 s2=27 s3=19 d 1=22 d 2=13 d3=12 d4=13 s 1=14 供应量 供应地 运价 需求量 需求地 675 3842759 106

运输问题线性规划模型 mnZ=6x11+7x12+5x13+3x14+8x21+4x22+2x23+7x24+5x31+9X32+10x33+6x34 S.tX1+X12+X13+X14 =14 X21+X22+X23+X24 =27 X31+X32+X3+X34 =19 供应地约束 X 十X21 +X31 =22 +X22 +X32 -15 X13 十X3 +X33 =12 需求地约束 X14 +X24 +X34 =13 X11X12X13X14X21X2X23 X24X31X32X3X34 ≥0 min 一般情形:有m x20 =∑%,∑4cx) 各供应地,n个 5t. 需求地,则有 ∑%xy=ayj=1,2,…,n ∑x)=b,i=12,…,m
运输问题线性规划模型 x x x x x x x x x x x x 0 x x x 13 x x x 12 x x x 13 x x x 22 x x x x 19 x x x x 27 s.t. x x x x 14 min z 6x 7x 5x 3x 8x 4x 2x 7x 5x 9x 10x 6x 1 1 1 2 1 3 1 4 2 1 2 2 2 3 2 4 3 1 3 2 3 3 3 4 1 4 2 4 3 4 1 3 2 3 3 3 1 2 2 2 3 2 1 1 2 1 3 1 3 1 3 2 3 3 3 4 2 1 2 2 2 3 2 4 1 1 1 2 1 3 1 4 1 1 1 2 1 3 1 4 2 1 2 2 2 3 2 4 3 1 3 2 3 3 3 4 + + = + + = + + = + + = + + + = + + + = + + + = = + + + + + + + + + + + 供应地约束需求地约束 一般情形:有 m 各供应地, n 个 需求地,则有 x b i m s t x a j n z c x i nj i j i mi i j mi nj i j i j xij , 1,2, , . . , 1,2, , min = 11 1 1 0 = = = = == = =
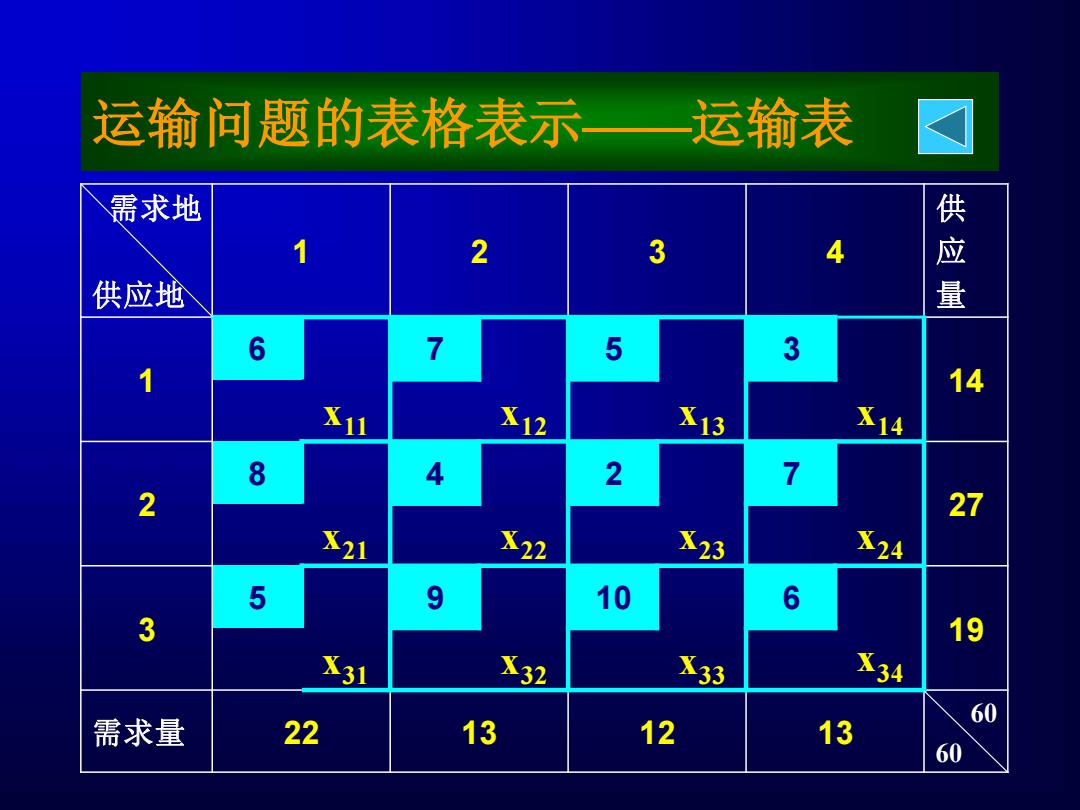
运输问题的表格表示—运输表 需求地 2 3 4 供应地 供应量 6 7 5 3 1 4 X12 X13 X14 8 4 2 7 2 27 X21 X22 X23 X24 5 9 10 6 3 19 X31 X32 X33 X34 60 需求量 22 13 12 13 60
运输问题的表格表示——运输表 需求地 供应地 1 2 3 4 供 应 量 1 6 7 5 3 14 x11 x12 x13 x14 2 8 4 2 7 27 x21 x22 x23 x24 3 5 9 10 6 19 x31 x32 x33 x34 需求量 22 13 12 13 60 60
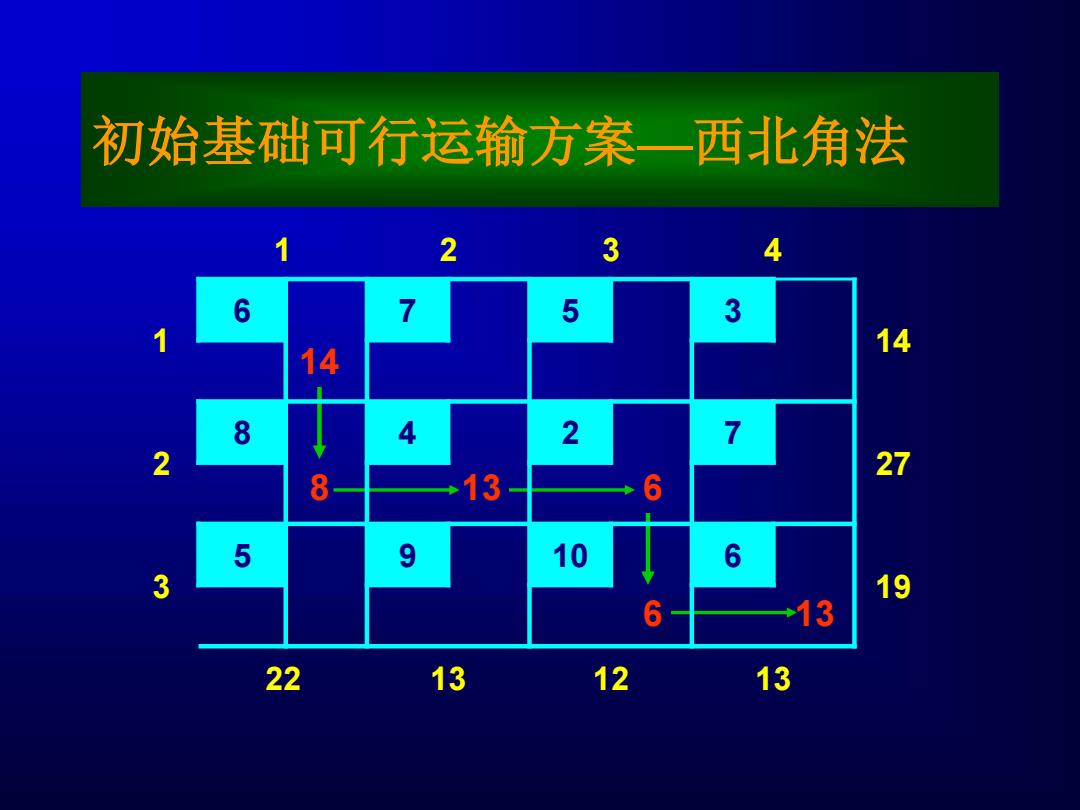
初始基础可行运输方案一西北角法 1 2 3 4 6 7 5 3 14 14 8 2 7 2 27 8 13 6 5 9 10 6 3 19 6 +13 22 13 12 13
初始基础可行运输方案—西北角法 8 13 13 14 6 6 1 2 3 4 1 6 7 5 3 14 2 8 4 2 7 27 3 5 9 10 6 19 22 13 12 13