
非线性规划理论与算法 ·非线性规划及其最优性条件 ·对偶理论 ·外点罚函数法 ·内点罚函数法 1
1 非线性规划理论与算法 • 非线性规划及其最优性条件 • 对偶理论 • 外点罚函数法 • 内点罚函数法

非线性规划 设x=(x1,,xn)I∈R”,f(x),C,(x):R”→R,i=1,2,,p+q,如下约束问 题称为非线性规划(Nonlinear Programming,NP): min f(x) min f(x) p=q=0即无约束规划 s.t.c,(x)≤0,i=1,,p x∈S c,(x)=0,i=p+1,,p+q 约束集或可行域:S={x∈R”c,(x)≤0,i=1,p,c,(x)=0,j=p+1,,p+q} x*是整体(全局)极小点台∈S,f(x)≥f(x*) x*是严格整体(全局)极小点台Vx∈S\{x,f(x)>f(x*) x*是局部极小点÷x∈Sn{x∈R”lx-x*<e},fx)之f(x*) x*是严格局部极小点台x∈Sn{x∈R”lIx-x<E,f(x)>f(*) 非线性规划向量化表示 令g(x)=(c(x,cn(x)》, min f(x) s.t. gy≤0 x)=(cp+1(x,cp+p(x》 3 h(x)=0
3 设 T n x = (x1 ,..., xn ) R , ( ), ( ) : n i f x c x R R , i p q = + 1,2, , ,如下约束问 题称为非线性规划(Nonlinear Programming, NP): min ( ) . . ( ) 0, 1,..., ( ) 0, 1,..., i i f x s t c x i p c x i p p q = = = + + ( ) 0, 1,..., , ( ) 0, 1,..., n 约束集或可行域: S x R c x i p c x j p p q = = = = + + i i 非线性规划 x*是整体(全局)极小点 x S f x f x , ( ) ( *) x*是严格整体(全局)极小点 x S x f x f x \ { }, ( ) ( *) x*是局部极小点 * , ( ) ( *) n − x S x R x x f x f x x*是严格局部极小点 * , ( ) ( *) n − x S x R x x f x f x min ( ) x S f x 1 1 ( ) ( ( ),..., ( )) , ( ) ( ( ),..., ( )) T p T p p p g x c x c x h x c x c x + + = = 令 min ( ) . . 0 ( ) 0 f x s t g(x) h x = 非线性规划向量化表示 p=q=0即无约束规划
非线性规划的几个概念 min f(x) 定义1.设f:R"→R,x∈R",d∈R",d≠0,若存在6>0,使 s.t.gx≤0 f(x+td)<f(x),t∈(0,δ) h(x)=0 则称向量d是函数fx)在点x处的下降方向。 d"vf(x)<0 定义2.设ScR,x∈S,deR",d≠0, 若存在t>0,使x+td∈S,则 称向量d是函数fx)在点x处关于S的可行方向。 线性化可行方向: 81(x)=0\ dVg,(x)≥0;drVh,(x)=0 可行方向锥 82(x)=0 4
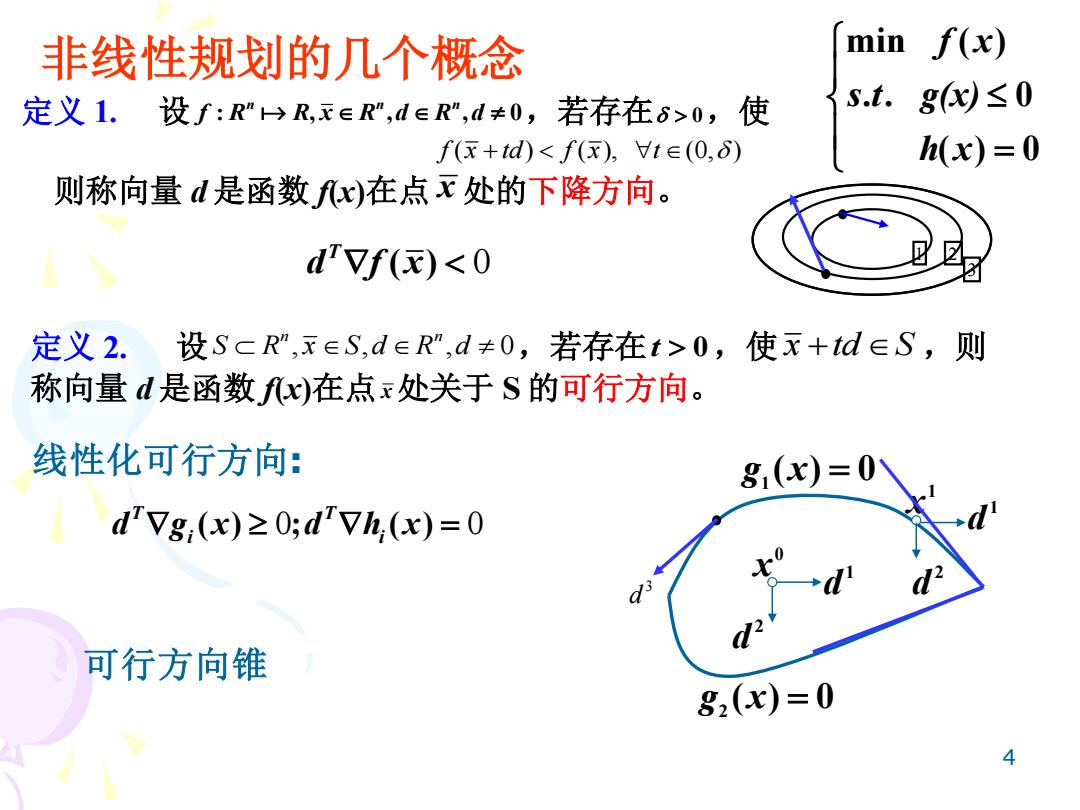
4 非线性规划的几个概念 定义 1. 设 : , , , 0 n n n f R R x R d R d ,若存在 0,使 f x td f x t ( ) ( ), (0, ) + 则称向量 d 是函数 f(x)在点 x 处的下降方向。 定义 2. 设 , , , 0 n n S R x S d R d ,若存在t 0,使 x td S + ,则 称向量 d 是函数 f(x)在点x处关于 S 的可行方向。 线性化可行方向: ( ) 0 T d f x ( ) ; ( ) 0 0 T T i i d g x d h x = min ( ) . . 0 ( ) 0 f x s t g(x) h x = g1 (x) = 0 g2 (x) = 0 0 x 1 x 1 d 1 d 2 d 2 d 1 2 3 3 d 可行方向锥

min f(x) s.t.g≤0 定义3:积极约束: h(x)=0 设点x∈Q,对于不等式约束g,(x)≤0,如果g()=0, 则称g,(x)≤0是点x处的积极约束。 或起作用约束(紧约束积极约束八有效约束) 。 记1()={ig,()=0,1≤i≤),称I()为点x处的积极约束指标集。 例:设g(x)=V2x2-x2≤0,8()=x2+x号-1≤0,8,()=-x≤0. 令x=(5,5y,则)=,24 2’2 x2 g2(x)=0 g1(x)=0 83(x)=0 5
5 定义3: 积极约束: , ( ) 0 ( ) 0, ( ) 0 i i i x Q g x g x g x x = 设点 对于不等式约束 ,如果 则称 是点 处的积极约束。 或起作用约束(紧约束\积极约束\有效约束)。 ( ) { | ( ) 0,1 }, ( ) i 记I x i g x i l I x x = = 称 为点 处的积极约束指标集。 2 2 2 1 1 2 2 1 2 3 1 ( ) 2 0, ( ) 1 0, ( ) 0 2 2 ( , ) ( ) 2 2 T g x x x g x x x g x x x I x = − = + − = − = = 例:设 . 令 ,则 {1,2}. 1 x 2 x O g2 (x) = 0 g1 (x) = 0 g3 (x) = 0 x min ( ) . . 0 ( ) 0 f x s t g(x) h x =

min f(x) 定理1: s.t.g(x≤0 给定点x∈Q,记点x的积极约束指标集为 I(x)。给定向量d, 如果对任意的i∈I(x)有Vg:(x)'d<0,则d是点x的可行方向。 证明:令x'=x+td,t>0。则对任意的i∈I(x),有 8(x')=g:(x)+t7gx)'d+o(td2) =tVg;(x)'d+o(ltd)<0 ∴.x'∈Q,即d为可行方向。 定义4:可行下降方向 设点x∈O,给定向量d,如果d既是点x处的可行方向, 又是该点的下降方向, 则称d为点x处的可行下降方向:
6 令 x'= x + t d ,t 0。则对任意的i I(x),有 ( ') ( ) ( ) (|| || ) 2 g x g x t g x d o td T i = i + i + ( ) (|| || ) 2 t g x d o td T = i + 0 x'Q,即d为可行方向。 又是该点的下降方向,则称 为点 处的可行下降方向。 设点 ,给定向量 ,如果 既是点 处的可行方向, d x x Q d d x 证明: 定理1: 定义4: 可行下降方向 如果对任意的 有 则 是 点 的可行方向。 给定点 记 点 的积极约束指标集为 。给定向量 , i I x g x d d x x Q x I x d T i ( ) ( ) 0, , ( ) min ( ) . . 0 f x s t g(x)