
第五章线性规划 ☒ 线性规划模型 ☑ 线性规划的图解 单纯形法原理 单纯形法 单纯形表 单纯形的理论分析 D人工变量法
1 第五章 线性规划 线性规划模型 线性规划的图解 单纯形法原理 单纯形法 单纯形表 单纯形的理论分析 人工变量法

§5.1孩性规划的数学摸型 一、问题的提出 例1:生产计划问题: 设备 A B C 利润 产 (元/公斤) 甲 3 5 9 70 乙 9 5 3 30 限制工时 540 450 720 间:甲乙各生产多少,使企业利阀最大? 2
2 §5.1 线性规划的数学模型 一、问题的提出 例1:生产计划问题: 问:甲乙各生产多少,使企业利润最大? 设备 产品 A B C 利润 (元/公斤) 甲 3 5 9 70 乙 9 5 3 30 限制工时 540 450 720
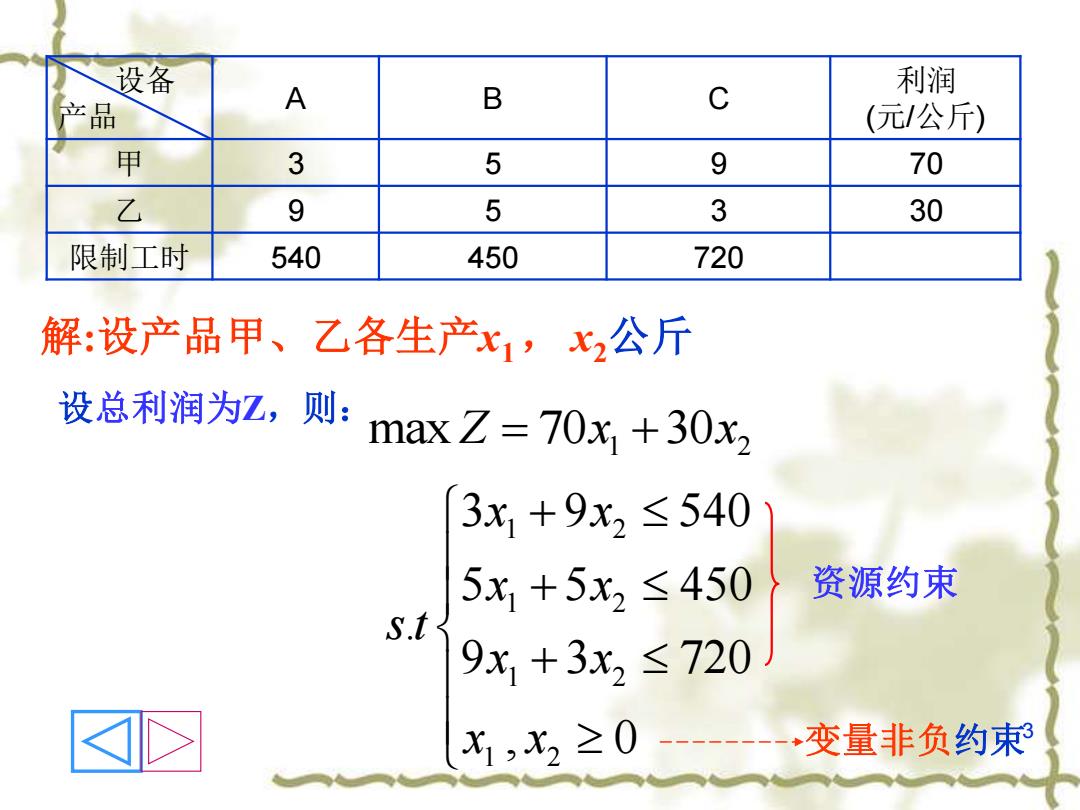
设备 A C 利润 产 B (元/公斤) 甲 3 5 9 70 乙 9 5 3 30 限制工时 540 450 720 解:设产品甲、乙各生产x1,x2公斤 设总利润为Z,则:maxZ=70x1+30x2 3x1+9x2≤540 5x+5x2≤450 资源约束 s.t 9x,+3x2≤720 X1,x2≥0 ----变量非负约束3
3 解:设产品甲、乙各生产x1, x2公斤 max 70 30 Z x x = +1 2 1 2 1 2 1 2 1 2 3 9 540 5 5 450 . 9 3 720 , 0 x x x x s t x x x x + + + 设总利润为Z,则: 设备 产品 A B C 利润 (元/公斤) 甲 3 5 9 70 乙 9 5 3 30 限制工时 540 450 720 资源约束 变量非负约束
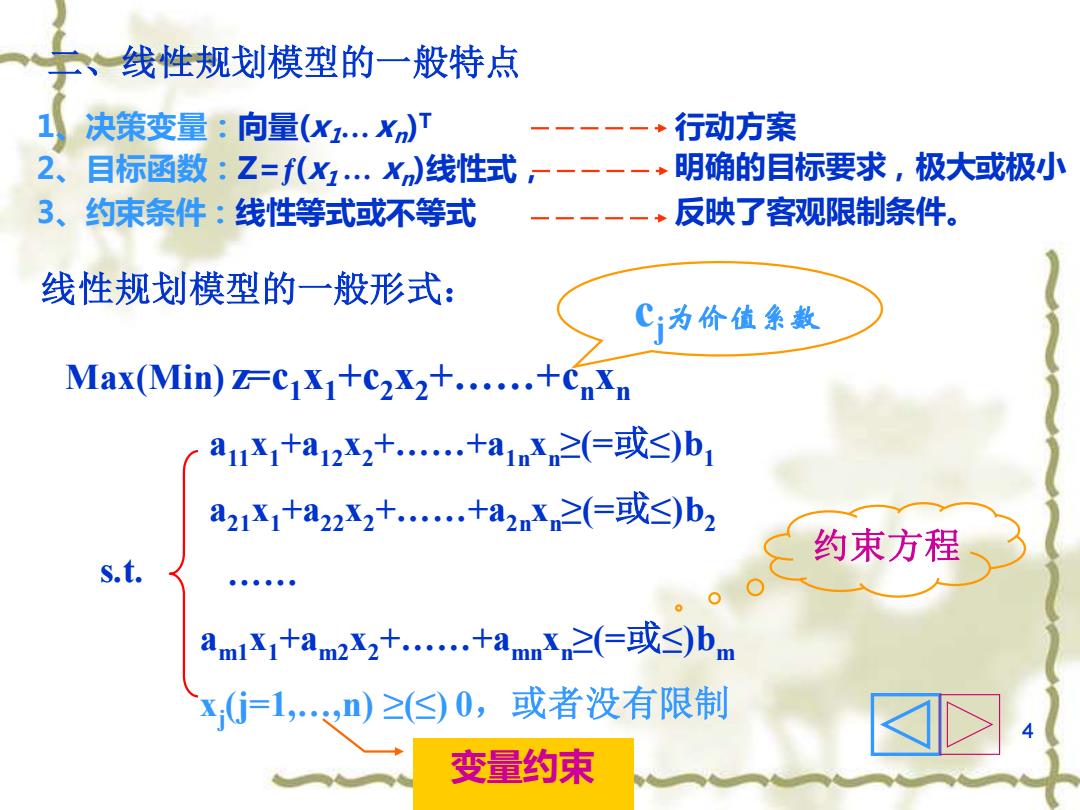
线性规划模型的一般特点 1 决策变量:向量(X…X)T 行动方案 2、 目标函数:Z=f(X1…X)线性式 一一一一一+明确的目标要求,极大或极小 3、 约束条件:线性等式或不等式 反映了客观限制条件。 线性规划模型的一般形式: C为价值集数 Max(Min)zcXj+c2X2+......+cnXn a1X1+a12X2+..+a1nx≥(=或≤)b1 a2X+a22x2+..+a2mX≥(=或≤)b2 约束方程 s.t. amlX+am2X2+..+ammX.≥(=或≤)bm Xj=1,n)≥()0, 或者没有限制 变量约束
4 二、线性规划模型的一般特点 Max(Min) z=c1 x1+c2 x2+……+cn xn a11x1+a12x2+……+a1n xn ≥(=或≤)b1 a21x1+a22x2+……+a2n xn ≥(=或≤)b2 …… am1 x1+am2 x2+……+amnxn ≥(=或≤)bm xj (j=1,…,n) ≥(≤) 0,或者没有限制 s.t. cj为价值系数 反映了客观限制条件。 明确的目标要求,极大或极小 行动方案 线性规划模型的一般形式: 1、决策变量:向量(x1…xn ) T 2、目标函数:Z=ƒ(x1… xn )线性式, 3、约束条件:线性等式或不等式 变量约束 约束方程
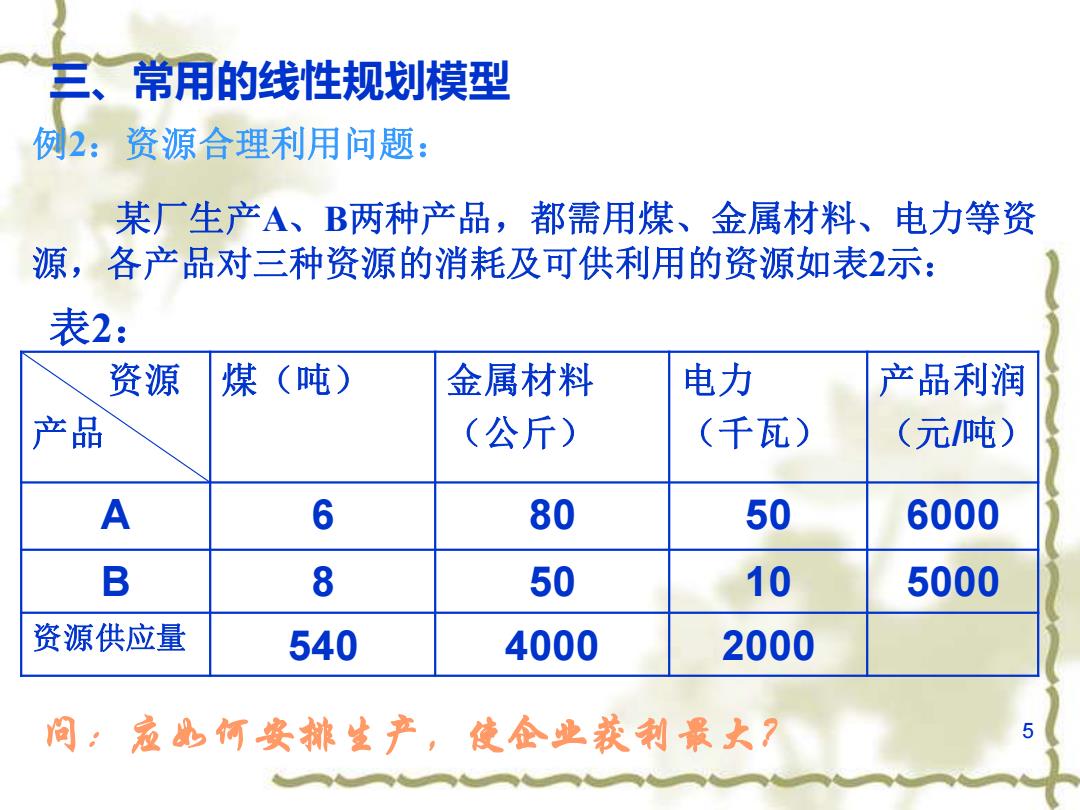
三、常用的线性规划模型 例2:资源合理利用问题: 某厂生产A、B两种产品,都需用煤、金属材料、电力等资 源,各产品对三种资源的消耗及可供利用的资源如表2示: 表2: 资源 煤(吨) 金属材料 电力 产品利润 产品 (公斤) (千瓦) (元吨) A 6 80 50 6000 B 8 50 10 5000 资源供应量 540 4000 2000 间:寇品何安排生产,使企业获利最大?
5 资源 产品 煤(吨) 金属材料 (公斤) 电力 (千瓦) 产品利润 (元/吨) A 6 80 50 6000 B 8 50 10 5000 资源供应量 540 4000 2000 表2: 例2:资源合理利用问题: 某厂生产A、B两种产品,都需用煤、金属材料、电力等资 源,各产品对三种资源的消耗及可供利用的资源如表2示: 问:应如何安排生产,使企业获利最大? 三、常用的线性规划模型