
第三章常用的一维搜索方法 3.1搜索算法结构 一、下降算法模型 minf) 考虑(NP) s.t.xES k+2 常用一种线性搜索的方式来求解:迭代中从 一点出发沿下降可行方向找一个新的、性 Y+ 质有改善的点。迭代计算: xk+1=x+入d,k=0,1,2,… 其中d为第k+1次迭代的搜索方向,2为沿d 搜索的最佳步长因子(通常也称作最佳步 长)
3.1 搜索算法结构 一、下降算法模型 考虑(NP) 常用一种线性搜索的方式来求解:迭代中从 一点出发沿下降可行方向找一个新的、性 质有改善的点。迭代计算: 其中 为第 次迭代的搜索方向, 为沿 搜索的最佳步长因子(通常也称作最佳步 长)。 min f(x) s.t. x∈S 第三章 常用的一维搜索方法 k d k +1 k k d 1 , 0,1,2, k k k k x x d k + = + = k X k+1 X k+2 X k 1 d + k d k 2 d + k k d

△下降方向 设x∈S,d∈R",d0,若存在δ>O, 使f(x+2.d)<f(x),V2∈(0,δ) ,称d为在x点的下 降方向。 △可行方向:设x∈S,d∈Rm,d0,若存在δ>O, 使x+入l∈S,V入∈(O,δ),称d为x点的可 行方问。 同时满足上述两个性质的方向称下降可行方向
△可行方向:设 ∈S,d∈Rn ,d≠0,若存在 , 使 ,称d 为 点的可 行方向。 同时满足上述两个性质的方向称下降可行方向。 _ x _ x _ x 0 , (0, ) _ x+ d S △下降方向 : 设 ∈S,d ∈Rn ,d≠0,若存在 , 使 ,称d 为 在 点的下 降方向。 0 ( ) ( ), (0, ) _ _ f x+ d f x _ x
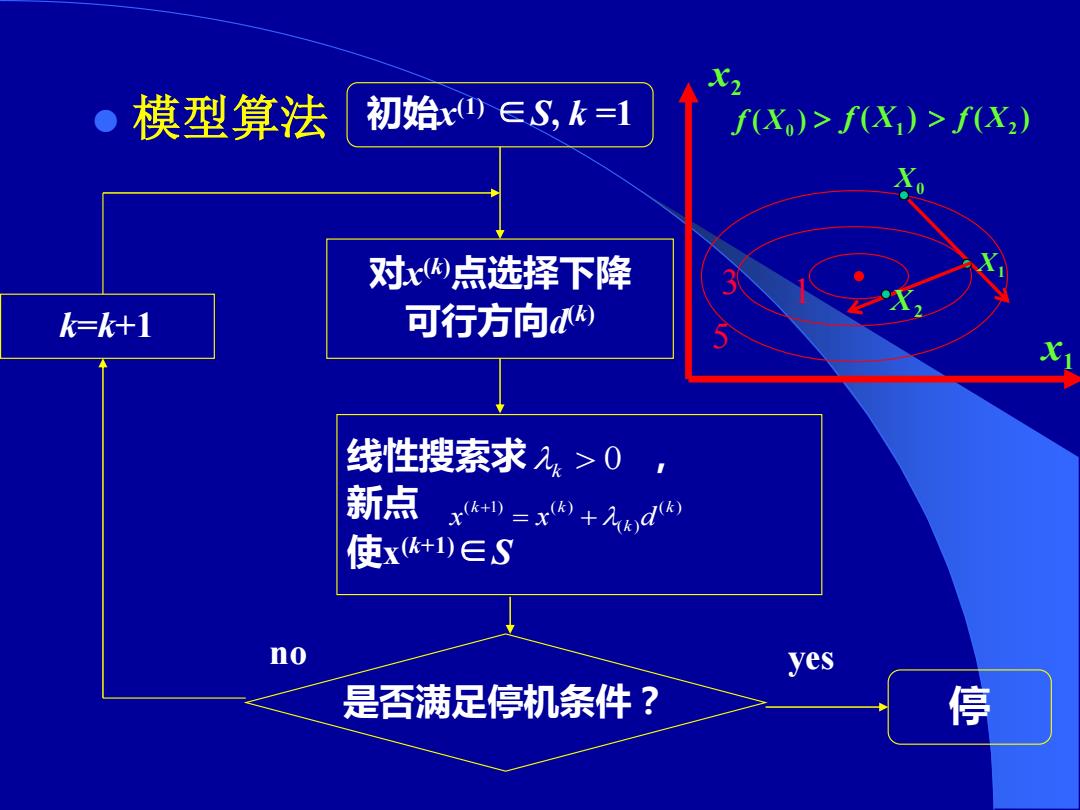
模型算法 初始x∈S,k=1 f(X)>f(X)>f(X,) X 对x点选择下降 k=k+1 可行方向 线性搜索求2>0 新点 x*+=x+2d 使xk+1)∈S no yes 是否满足停机条件? 停
⚫ 模型算法 线性搜索求 , 新点 使x (k+1)∈S 初始x (1) ∈S, k =1 对x (k)点选择下降 可行方向d (k) k 0 ( ) ( ) ( 1) ( ) k k k k x = x + d + 是否满足停机条件? 停 k=k+1 no yes x1 x2 5 3 1 X0 X1 X2 ( ) X0 f ( ) X1 f ( ) X2 f

二、收敛性概念: 考虑(NP) min fx s.t,x∈S 设迭代算法产生点列xcS. 1.理想的收敛性:设x*∈S是g.op(全局最优 解)当x*∈{x或xk)≠x*,k,满足 lim x()=x k>o∞ 时,称算法收敛到最优解x*
二、收敛性概念: 考虑(NP) 设迭代算法产生点列{x (k) } S. 1. 理想的收敛性:设x*∈S是g.opt(全局最优 解).当x*∈ {x (k) } 或 x (k) ≠ x* , k,满足 时,称算法收敛到最优解 x* 。 ( ) * lim x x k k = → min f(x) s.t. x∈S

由于非线性规划问题的复杂性,实用中建立下列收 敛性概念: 2.实用收敛性:定义解集 S*={xx具有某种性质} 例:S*={xx-g.0p S*={xx---L.opty S*=x!x)=) S*=x)s}(B为给定的实数阈值
由于非线性规划问题的复杂性,实用中建立下列收 敛性概念 : 2. 实用收敛性:定义解集 S* = { x | x 具有某种性质 } 例:S*={x|x---g.opt} S*={x|x---l.opt} S*={x| f(x)=0} S*={x|f(x)≤β } (β为给定的实数阈值)