
5.多目标规划 多目标规划建模一引例 多目标规划模型 多目标规划的示意图 ☒ 多目标规划的性质 ☑ 多目标规划重要算法 用MATLAB解无约束规划
5. 多目标规划 多目标规划建模——引例 多目标规划模型 多目标规划的示意图 多目标规划的性质 多目标规划重要算法 用MATLAB解无约束规划

引例1:投资问题 某公司在一段时间内有(亿元)的资金可用于建厂投资。 若可供选择的项目记为1,2,.,m。而且一旦对第i个项目 投资,就用去a亿元;而这段时间内可得收益c亿元。问如 何如确定最佳的投资方案? 对第个项目投资 xi= 0 不对第个项目投资 约束条件为: J∑ax,≤a 双目标规划 x,(1-x)=0,i=1,2,m 最佳的投资方案— 投资最少、收益最大 投资最少:mimf(化,七,,xn)=∑1,y 收益最大 max2(比,X2,,xn)=∑21cy
引例1: 投资问题 某公司在一段时间内有a(亿元)的资金可用于建厂投资。 若可供选择的项目记为1,2,...,m。而且一旦对第i个项目 投资,就用去ai亿元;而这段时间内可得收益ci亿元。问如 何如确定最佳的投资方案? ( ) − = = = x x i m a x a i i m i i i 1 0, 1,2, , 1 = 0 1 i x 对第i个项目投资 不对第i个项目投资 约束条件为: 最佳的投资方案——投资最少、收益最大 投资最少: = = m i x x xm ai xi f 1 1 1 2 min ( , ,, ) 收益最大 = = m i m i xi f x x x c 1 2 1 2 max ( , ,, ) 双目标规划

引例2:生产问题 某工厂生产两种产品,产品A每单位利润为10元,而产品B 每单位利润为8元,产品A每单位需3小时装配时间而B为2小时, 每周总装配有效时间为120小时。工厂允许加班,但加班生产 出来的产品利润的减去1元,根据最近的合同,厂商每周最少 得向用户提供两种产品各30单位。要求:1)必须遵守合同;2) 尽可能少加班;3)利润最大.问怎样安排生产? 每周正常时间生产得A产品数量一x1 约束条件为: 每周加班时间生产得A产品数量一x2 X1+x2≥30 每周正常时间生产得B产品数量 -X3 x3+x4≥30 每周加班时间生产得B产品数量一x4 3x1+2x3≤120 加班最少 利润最大 x,≥0 min 3.x2+2x max10x1+9x2+8x3+7x4
引例2: 生产问题 某工厂生产两种产品,产品A每单位利润为10元,而产品B 每单位利润为8元,产品A每单位需3小时装配时间而B为2小时, 每周总装配有效时间为120小时。工厂允许加班,但加班生产 出来的产品利润的减去1元,根据最近的合同,厂商每周最少 得向用户提供两种产品各30单位。要求:1) 必须遵守合同;2) 尽可能少加班;3)利润最大.问怎样安排生产? + + + 0 3 2 120 30 30 1 3 3 4 1 2 xi x x x x x x 约束条件为: 加班最少 min 3x2 + 2x4 利润最大 max 10x1 + 9x2 + 8x3 + 7x4 每周正常时间生产得A产品数量——x1 每周正常时间生产得B产品数量——x3 每周加班时间生产得A产品数量——x2 每周加班时间生产得B产品数量——x4

多目标规划的模型 般形式: mimi(X),f(X),f,(X》 X∈R" g(X)0 j=1,2,..,m; s.t. h(X)=0k=1,2,l. 函数f,8,h,满足 f:R”→R, 8:R”→R,:R"→R,p≥2 求目标函数的最大值或约束条件为大于等于零的情况,都 可通过取其相反数化为上述一般形式
多目标规划的模型 一般形式: V- f (X) f (X) f p (X) X R n min , , , 1 2 ( ) ( ) = = = 0 1,2,..., . 0 1,2,..., ; . . h X k l g X j m s t k j 函 数f i , g j ,hk 满 足 f : R R, g : R R, h : R R, n k n j n i → → → 求目标函数的最大值或约束条件为大于等于零的情况,都 可通过取其相反数化为上述一般形式. p 2
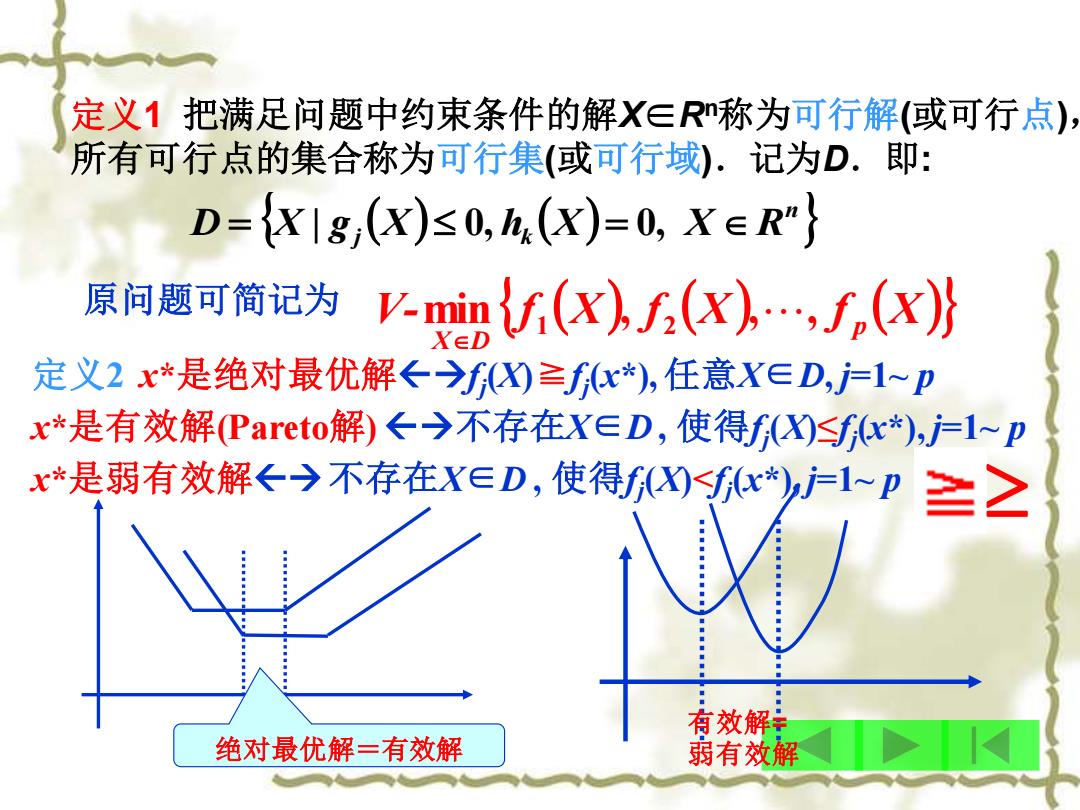
定义1把满足问题中约束条件的解X∈称为可行解(或可行点) 所有可行点的集合称为可行集(或可行域).记为D.即: D=x1g,(x)30,(X)=0,XER" 原问题可简记为 v-mintf(x)(x).(x) X∈D 定义2x*是绝对最优解←→fX)≥fx*),任意X∈D,=1~p x*是有效解Paretof解)←→不存在X∈D,使得f)Sfc*),户l~p x*是弱有效解←→不存在X∈D,使得)fx*j户1~p ≥之 有效解: 绝对最优解=有效解 弱有效解
( ) ( ) n D = X | gj X 0, hk X = 0, X R 定义1 把满足问题中约束条件的解X∈Rn称为可行解(或可行点), 所有可行点的集合称为可行集(或可行域).记为D.即: 原问题可简记为 定义2 x*是绝对最优解→fj (X)≧fj (x*), 任意X∈D, j=1~ p x*是有效解(Pareto解) →不存在X∈D , 使得fj (X)≤fj (x*), j=1~ p x*是弱有效解→不存在X∈D , 使得fj (X)<fj (x*), j=1~ p V- f (X) f (X) f p (X) X D min , , , 1 2 绝对最优解=有效解 有效解= 弱有效解