
数学建模讲义 →优化模型
数学建模讲义 →优化模型

1、线性规划 2、线性整数规划 3、运输问题 4、无约束规划 5、多目标规划 6、非线性规划 7、动态规划 ■■
1、线性规划 5、多目标规划 6、非线性规划 7、动态规划 ……… 2、线性整数规划 4、无约束规划 3、运输问题

1.线性规划 线性规划建模一 引例 线性规划模型 线性规划的图解 线性规划的性质 线性规划重要算法 用MATLAB解线性规划
1. 线性规划 线性规划建模——引例 线性规划模型 线性规划的图解 线性规划的性质 线性规划重要算法 用MATLAB解线性规划

例1:一某厂每日8小时的产量不低于1800件。为了进行质 量控制,计划聘请两种不同水平的检验员。一级检验员的标准 为:速度25件/小时,正确率98%,计时工资4元/小时;二级检 验员的标准为:速度15小时/件,正确率95%,计时工资3元/小 时。检验员每错检一次,工厂要损失2元。为使总检验费用最 省,该工厂应聘一级、二级检验员各几名? 解 设需要一级和二级检验员的人数分别为x1、X2人,则应付 检验员的工资为: 8×4×x1+8×3×X2=32x1+24x2 因检验员可能错检而造成的损失为: (8×25×2%×x1+8×15×5%×x2)×2=8x1+12x2 故目标函数为: min Z=40x +36x2 约束条件为: s.t.5x1+3x2≥45 x1≤9,x2≤15 x1≥0,X2≥0
引例1: 某厂每日8小时的产量不低于1800件。为了进行质 量控制,计划聘请两种不同水平的检验员。一级检验员的标准 为:速度25件/小时,正确率98%,计时工资4元/小时;二级检 验员的标准为:速度15小时/件,正确率95%,计时工资3元/小 时。检验员每错检一次,工厂要损失2元。为使总检验费用最 省,该工厂应聘一级、二级检验员各几名? 解 设需要一级和二级检验员的人数分别为x1、x2人, 则应付 检验员的工资为: 84x1 + 83x2 = 32x1 + 24x2 因检验员可能错检而造成的损失为: 1 2 2 8x1 12x2 (8252%x + 8155%x ) = + 故目标函数为: 40x1 36x2 min z = + 约束条件为: x 0, x 0 x 9, x 15 s.t. 5x 3x 45 1 2 1 2 1 2 +
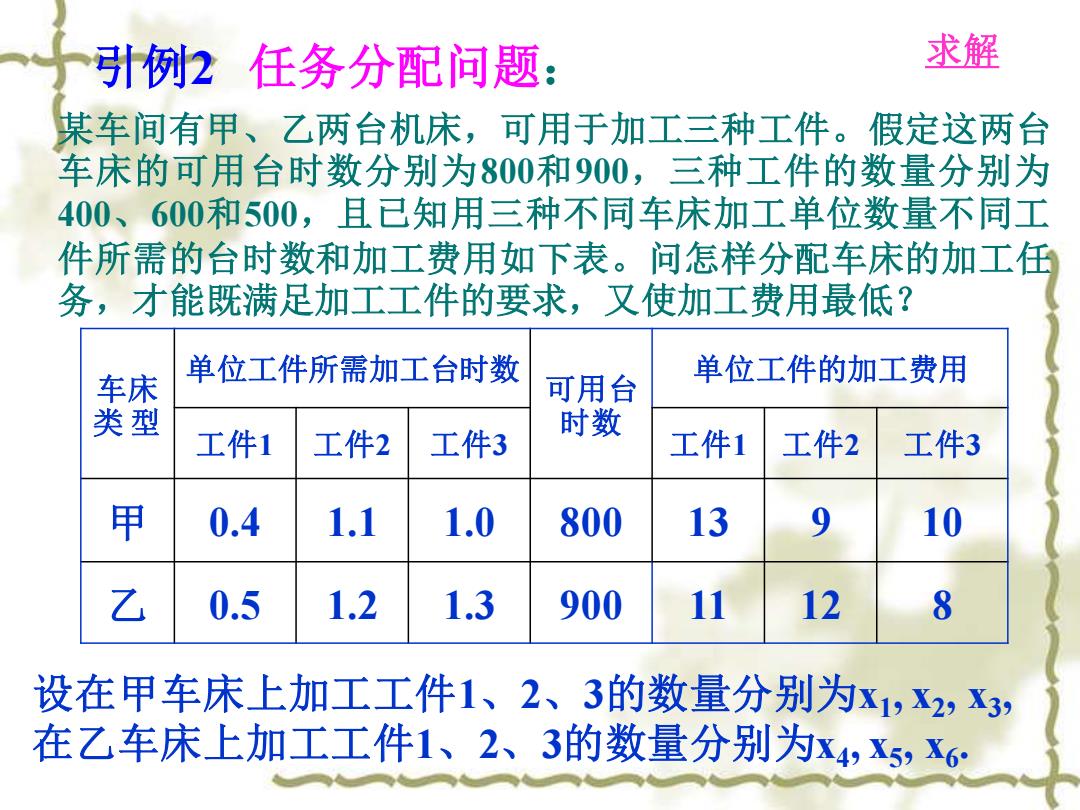
引例2任务分配问题: 求解 某车间有甲、乙两台机床,可用于加工三种工件。假定这两台 车床的可用台时数分别为800和00,三种工件的数量分别为 400、600和500,且已知用三种不同车床加工单位数量不同工 件所需的台时数和加工费用如下表。问怎样分配车床的加工任 务,才能既满足加工工件的要求,又使加工费用最低? 车床 单位工件所需加工台时数 单位工件的加工费用 可用台 类型 工件1 工件2 工件3 时数 工件1 工件2 工件3 甲 0.4 1.1 1.0 800 13 9 10 0.5 1.2 1.3 900 11 12 8 设在甲车床上加工工件1、2、3的数量分别为x1,X2,X3, 在乙车床上加工工件1、2、3的数量分别为x4,X5,6
某车间有甲、乙两台机床,可用于加工三种工件。假定这两台 车床的可用台时数分别为800和900,三种工件的数量分别为 400、600和500,且已知用三种不同车床加工单位数量不同工 件所需的台时数和加工费用如下表。问怎样分配车床的加工任 务,才能既满足加工工件的要求,又使加工费用最低? 引例2 任务分配问题: 车床 类 型 单位工件所需加工台时数 可用台 时数 单位工件的加工费用 工件1 工件2 工件3 工件1 工件2 工件3 甲 0.4 1.1 1.0 800 13 9 10 乙 0.5 1.2 1.3 900 11 12 8 设在甲车床上加工工件1、2、3的数量分别为x1 , x2 , x3 , 在乙车床上加工工件1、2、3的数量分别为x4 , x5 , x6 . 求解