
第四章 无约束非线性问题的解法 本章要点: >最速下降法的基本思想及特点 min f(x) x∈R” >牛顿方向 >Newton法基本思想及特点 >共轭方向、共轭方向法的基本定理 >共轭梯度法基本思想 >拟Newton法的基本思想
本章要点: ➢最速下降法的基本思想及特点 ➢牛顿方向 ➢Newton法基本思想及特点 ➢共轭方向、共轭方向法的基本定理 ➢共轭梯度法基本思想 ➢拟Newton法的基本思想 第四章 无约束非线性问题的解法 min ( ) n x R f x

学习的重要性: 1、直接用于无约束的实标问题; 2、其基本思想和逻辑结构可以推广到约束问题: 3、约束问题可以转化成无约束问题求解。 方法分类: 1、间接法:对简单问题,求解必要条件或充分条件; 零阶法:只需计算函数值x) 直接法 2、迭代算法: 一阶法:需计算Vfx) 梯度法 二阶法:需计算V2x)
学习的重要性: 1、直接用于无约束的实际问题; 2、其基本思想和逻辑结构可以推广到约束问题; 3、约束问题可以转化成无约束问题求解。 方法分类: 1、间接法:对简单问题,求解必要条件或充分条件; 2、迭代算法: 零阶法:只需计算函数值f(x) 一阶法:需计算▽f(x) 二阶法:需计算▽2 f(x) 直接法 梯度法

考虑无约束优化问题: min f(x) xERT 本章主要介绍无约束最优化方法,它的应用比较广泛,理论比较 成熟。另一方面,通常可以把一些约束优化问题转化为无约束问题来 处理,所以它是最优化方法中的基本方法。 这些方法通常要用到函数的一阶或二阶导数。 在实际问题中,也常遇到函数的解析表达式比较复杂,有的甚至 写不出明显的解析表达式,因而导数很难求出或无法求出,这时基于 梯度的方法不能用,需要采取另一种所谓的直接法(或直接搜索法)。 直接法是仅仅利用函数值的信息,去寻找最优解的一类方法。在后面 第九章有介绍
本章主要介绍无约束最优化方法,它的应用比较广泛,理论比较 成熟。另一方面,通常可以把一些约束优化问题转化为无约束问题来 处理,所以它是最优化方法中的基本方法。 这些方法通常要用到函数的一阶或二阶导数。 在实际问题中,也常遇到函数的解析表达式比较复杂,有的甚至 写不出明显的解析表达式,因而导数很难求出或无法求出,这时基于 梯度的方法不能用,需要采取另一种所谓的直接法(或直接搜索法)。 直接法是仅仅利用函数值的信息,去寻找最优解的一类方法。在后面 第九章有介绍。 考虑无约束优化问题: min ( ) n x R f x

直接搜索法收敛速度一般比较慢,需要计算大量的函数值。 梯度反映了函数值变化的规律,充分利用梯度信息构造算法, 能加速收敛。 使用函数的梯度(一阶导数)或Hesse矩阵 (二阶导数)的 优化算法统称为梯度法。 算法目标:求出平稳点(满足又fx)=O的x*)。 由于Vfx)=0一般是非线性方程组,解析法往往行不通 所以梯度法通常是逐次逼近的迭代法。 假定:7fx)和72fx)连续存在
直接搜索法收敛速度一般比较慢,需要计算大量的函数值。 梯度反映了函数值变化的规律,充分利用梯度信息构造算法, 能加速收敛。 使用函数的梯度(一阶导数)或Hesse矩阵(二阶导数)的 优化算法统称为梯度法。 算法目标:求出平稳点 (满足f(x)=0的x * )。 由于 f(x)=0 一般是非线性方程组,解析法往往行不通, 所以梯度法通常是逐次逼近的迭代法。 假定: f(x)和 2 f(x)连续存在
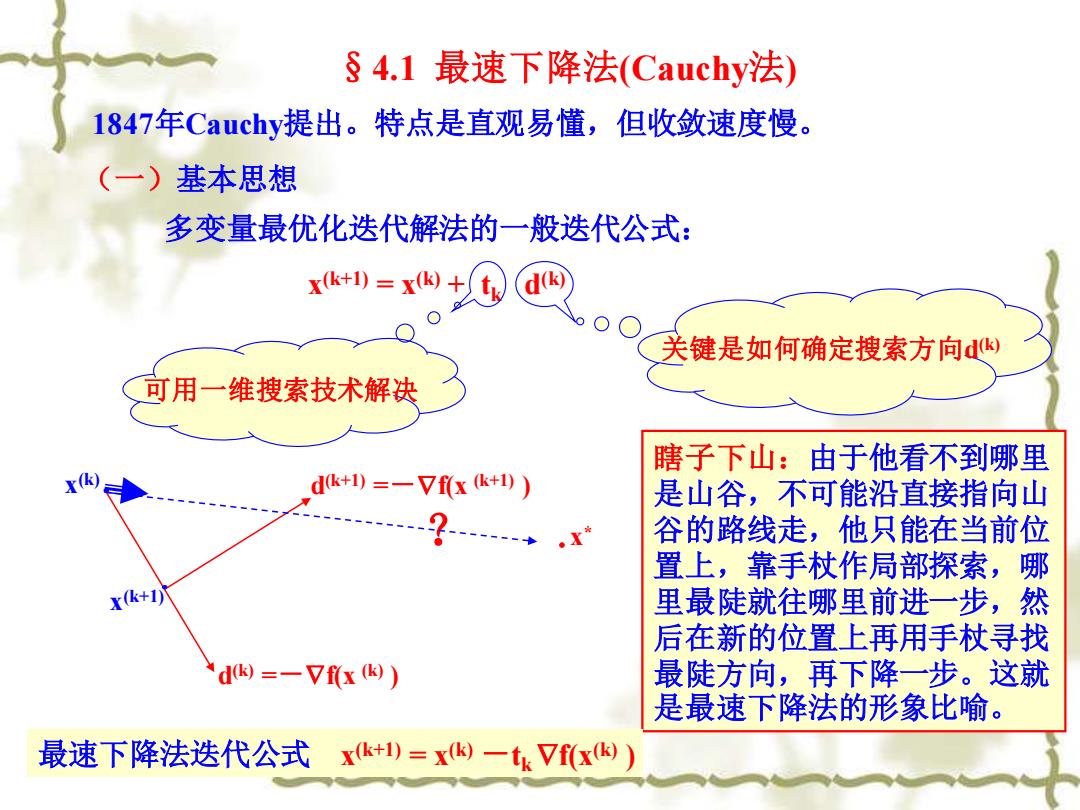
§4.1最速下降法(Cauchy法) 1847年Cauchy提出。特点是直观易懂,但收敛速度慢。 (一)基本思想 多变量最优化迭代解法的一般迭代公式: xk+I)=x+以 关键是如何确定搜索方向d 可用一维搜索技术解决 瞎子下山:由于他看不到哪里 dk+)=一Vfxk+) 是山谷,不可能沿直接指向山 ? 谷的路线走,他只能在当前位 置上,靠手杖作局部探索,哪 里最陡就往哪里前进一步,然 后在新的位置上再用手杖寻找 d(k)=-Vf(x (k) 最陡方向,再下降一步。这就 是最速下降法的形象比喻。 最速下降法迭代公式xk+=xW一t7f(x)
§4.1 最速下降法(Cauchy法) (一)基本思想 x (k+1) = x(k) + tk d (k) x (k) x * d (k) =-f(x (k) ) x (k+1) d (k+1) =-f(x (k+1) ) 瞎子下山:由于他看不到哪里 是山谷,不可能沿直接指向山 谷的路线走,他只能在当前位 置上,靠手杖作局部探索,哪 里最陡就往哪里前进一步,然 后在新的位置上再用手杖寻找 最陡方向,再下降一步。这就 是最速下降法的形象比喻。 ? 多变量最优化迭代解法的一般迭代公式: 可用一维搜索技术解决 关键是如何确定搜索方向d (k) 最速下降法迭代公式 x (k+1) = x(k) -tk f(x(k) ) 1847年Cauchy提出。特点是直观易懂,但收敛速度慢