特殊矢量场 ■有势场 A=grad u 4=-grad v rotA=0 u(x,V,)= Px,y。,o)dk+ Q(x。)dh+ R(x,y,a)d追 ◆ 管形场 di4=0 =0x片)- R(x,y,o)dy V=-[P(x,y,2)da A≡rOtB W=C(C为任何常数 调和场 divA=0 x,y)=-P(x,)d- O(x,y)dy rot4=0 e(x,y.)dxP(x,y)dy lexu@mail.xidian.edu.cn
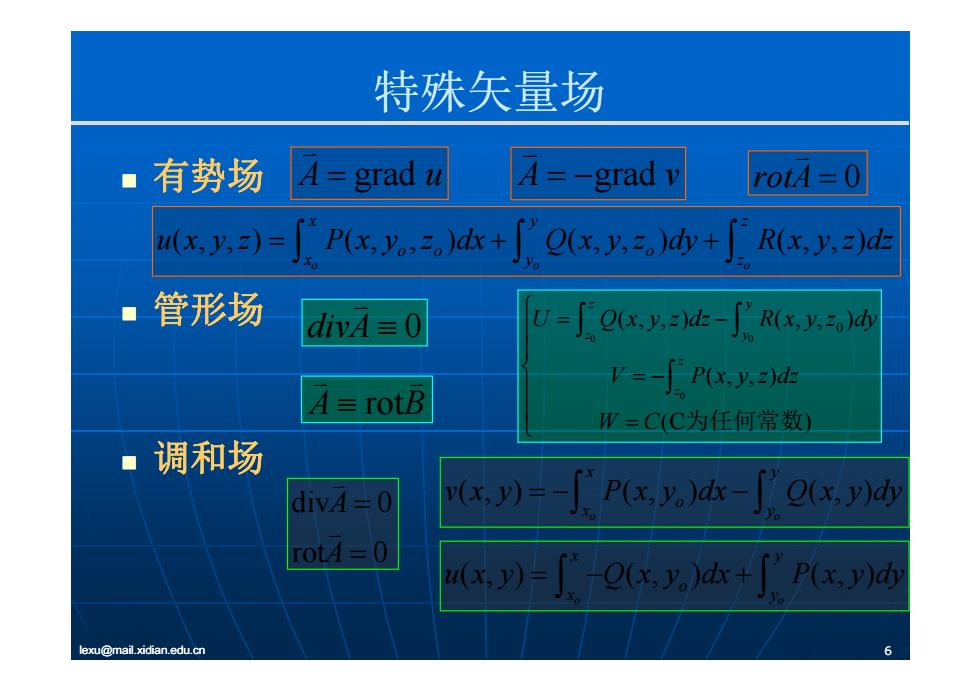
特殊矢量场 有势场 A grad u A grad v rotA 0 有势场 g g (, ,) (, , ) (, , ) (, ,) o oo x yz oo o x y z u x y z Px y z dx Q x y z dy R x y z dz 管形场 o oo y divA 0 0 0 0 (, ,) (, , ) z y z y U Q x y z dz R x y z dy A rotB 0 (, ,) (C ) z z V P x y z dz W C 为任何常数 调和场 W C (C ) 为任何常数 div 0 A (, ) (, ) (, ) x y o v x y P x y dx Q x y dy div 0 rot 0 A A (, ) (, ) (, ) o o o x y y y Q yy (, ) (, ) (, ) x y u x y Q x y dx P x y dy lexu@mail.xidian.edu.cn 6 (, ) (, ) (, ) o o o x y u x y Q x y dx P x y dy
特殊矢量场 ■共轭调和 Ou bv Ou ov 共轭调和条件 ox ay'dy dx O'uo'u =0 共轭调和函数 =0 O a2 2 ■拉普拉斯算子 △三 拉普拉逊 调和量 满足拉普拉斯 △u=div(grad 方程,且有二 阶连续偏导数 ■拉普拉斯方程 △2u=0 的函数,叫做 调和函数 lexu@mail.xidian.edu.cn
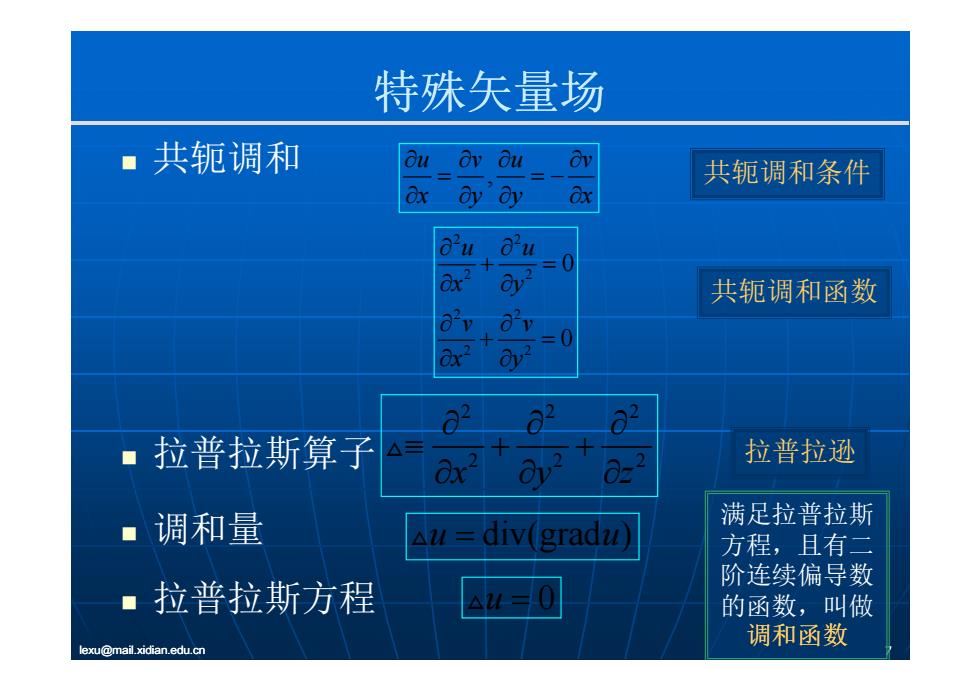
特殊矢量场 共轭调和 , u vu v 共轭调和条件 x yy x 2 2 0 u u 2 2 2 2 2 2 0 0 x y v v 共轭调和函数 2 2 0 x y 222 拉普拉斯算子 222 xyz 拉普拉逊 满足拉普拉斯 调和量 拉普拉斯 u u div(grad ) 满足拉普拉斯 方程,且有二 阶连续偏导数 lexu@mail.xidian.edu.cn 7 拉普拉斯方程 u 0 阶连续偏导数 的函数,叫做 调和函数
哈密顿算子 微分性 矢量性 。V算子一哈密顿算子 Nabla(那勃勒) ·直角坐标系定义: Del代尔) 。梯度: gradu Vu 数乘 ·散度: =7, 点积 ·旋度: rotM=7× 叉积 a -+4 +A lexu@mail.xidian.edu.cn
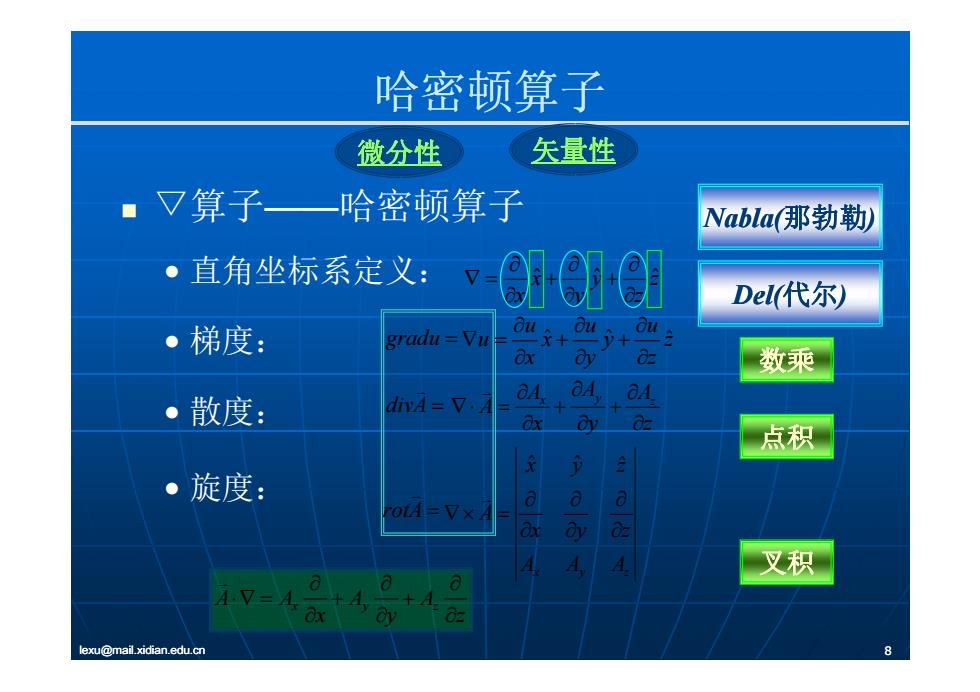
哈密顿算子 算 哈密顿算 微分性 矢量性 ▽算子——哈密顿算子 • 直角坐标系定义 Nabla(那勃勒) • 直角坐标系定义: • 梯度: z z y y x x ˆ ˆ ˆ ˆ ˆ ˆ uuu u xyz Del(代尔) • 梯度: gradu • 散度: u xyz x y z x y z A A A A xyz g divA 数乘 点 x y ˆ ˆ z ˆ 散度 • 旋度: xyz A 点积 x y z A x y z A A A rotA 叉积 lexu@mail.xidian.edu.cn 8 AA A A xyz x y z

哈密顿算子 ■两个矢量恒等式 div(rot④=0 7,(7×=0 旋无散 rot(gradu)=0 7×7=0 梯无旋 ■两个积分变换 A·d=rot·d ∮Adl=f ×Ad 线→面 乐A divAdy V.Adv 面→体 lexu@mail.xidian.edu.cn 9
哈密顿算子 两个矢量恒等式 ( ) div(rot ) 0 A ( ) A 0 旋无散 两个积分变换 rot(grad ) 0 u ( )0 u 梯无旋 两个积分变换 A dl A ds rot Adl A ds 线→面 A ds divAdv L S L S A d Ad 面 体 lexu@mail.xidian.edu.cn 9 S V A ds divAdv 面→体 S V A d s Adv