
第三章微分中值定理与导数的定用 第一节 微分中值定理 第二节泰勒(Taylor)公式 第三节 洛必达法则 第四节函数的单调性与曲线的凹凸性 第五节 函数的极值与最大值、最小值 第六节 函数图形的描绘 第七节曲率 2009年7月3日星期五 2 目录 上页 下页 返回
2009年7月3日星期五 2 目录 上页 下页 返回 第三章 微分中值定理与导数的应用 第三节 洛必达法则 第四节 函数的单调性与曲线的凹凸性 第五节 函数的极值与最大值、最小值 第六节 函数图形的描绘 第七节 曲率 第二节 泰勒 ( Taylor )公式 第一节 微分中值定理

第三章 第一节 微分中值定理 (The Mean Value Theorem) 一、函数的极值 罗尔中值定理 二、微分中值定理〈拉格朗日中值定理 柯西中值定理 三、小结与思考题 2009年7月3日星期五 3 目录○ 上页 下页 返回
2009年7月3日星期五 3 目录 上页 下页 返回 第一节 微分中值定理 第三章 二、微分中值定理 三、小结与思考题 (The Mean Value Theorem ) 罗尔中值定理 拉格朗日中值定理 柯西中值定理 一、函数的极值
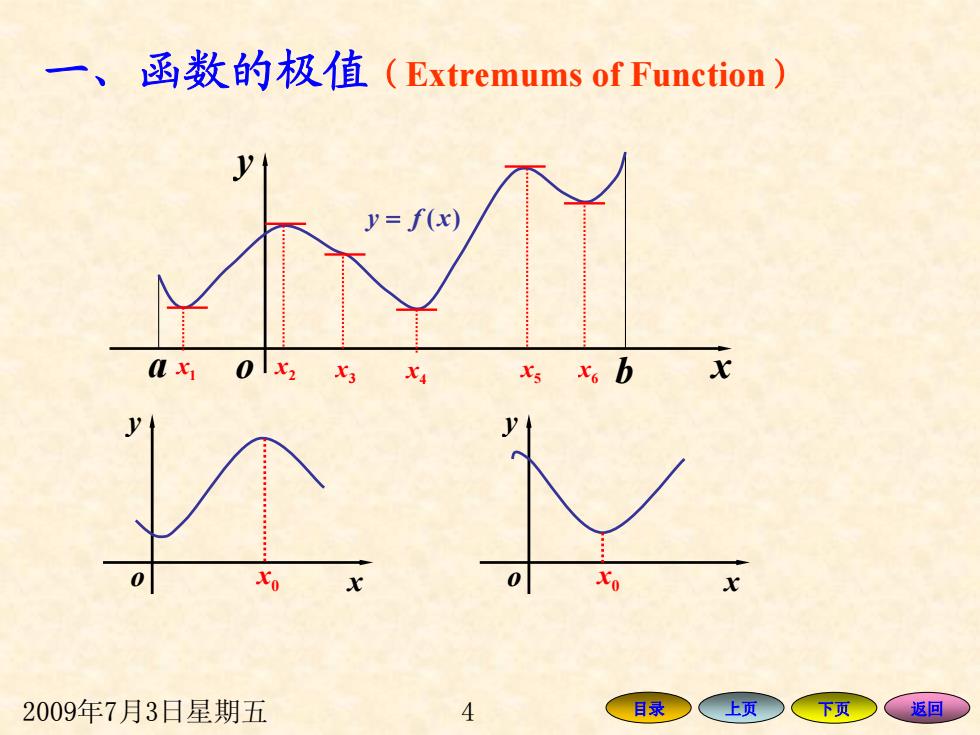
一、函数的极值(Extremums of Function) y=f(x) 01x2 0 2009年7月3日星期五 4 目录 上页 下页 、返回
2009年7月3日星期五 4 目录 上页 下页 返回 一、函数的极值 (Extremums of Function ) o x y a b y = f x)( x1 x2 x3 x 4 x5 x 6 o x y o x y 0 x 0 x

定义设函数f(x)在区间(a,b)内有定义,x是(a,b) 内的一,点,如果存在x。的一个邻域U(x),对于U(x)内 的任何点x,有 f(x)≤f(x)或f(x)≥f(x), 则称f(x)是函数f(x)的一个极大值(或极小值),点x 是f(x)的一个极大值点(或极小值点),函数的极大值、 极小值统称为极值极大值点与极小值点统称为极值点。 注意:函数的极大值、极小值与最大值、最小值的区 别.函数的极值是对一点的邻域来说的,是局部性概念; 而最值(最大值、最小值的简称)是整体性概念. 2009年7月3日星期五 5 目录 上页 下页 返回
2009年7月3日星期五 5 目录 上页 下页 返回 定义 设函数 f ( ) x 在区间(,) a b 内有定义, 0 x 是(,) a b 内的一点,如果存在 0 x 的一个邻域 0 U x( ),对于 0 U x( ) 内 的任何点 x ,有 0 fx fx () ( ) ≤ 或 0 fx fx () ( ) ≥ , 则称 0 f x( ) 是函数 f x( ) 的一个极大值(或极小值),点 0 x 是 f x( ) 的一个极大值点(或极小值点 ),函数的极大值、 极小值统称为极值 .极大值点与极小值点统称为极值点 . 注意:函数的极大值、极小值与最大值、最小值的区 别.函数的极值是对一点的邻域来说的,是局部性概念 ; 而最值(最大值、最小值的简称)是整体性概念.

费马引理(Fermat Lemma) y=x)在U(x)有定义,→f,)=0 马,P.d 且f(x)≤f(xo),∫'(x)存在 (或≥) 证:设Vxo+△x∈U(xo)f(x+△x)≤f(xo), f(x)lim f(o+Ax)-f(xo) 0X0X △x>0 △x '(xo)≥0(△x→0) f(xo)≤0(△x→0+) =+f()=0 证毕 2009年7月3日星期五 6 目录 上页 下页 返回
2009年7月3日星期五 6 目录 上页 下页 返回 费马引理 (Fermat Lemma ) ,)( 在 ∪ x 0 有定义 且 )( 0 f x ≤ f x 0 ,)()( f ′ x 存在 或 ≥)( 0)( f ′ x 0 = 证 : 设 ,)()(,)( 0 00 0 ∀ Δ+ ∈ ∪ xxx f + Δxx ≤ f x )( 0 则 f ′ x x f xx f x x Δ + Δ − = →Δ )()( lim 0 0 0 = )0( →Δ − f− ′ x 0 )( x )0( →Δ + f+ ′ x 0 )( x ≥ 0 ≤ 0 0)( f ′ x 0 = x y o 0 x y = f x)( 证毕