设平面曲线C是光滑曲线 y (即曲线C上每一点处都有切 线,且切线随切点的移动而连续 转动,M,是基点,MM=As, 价SM △0 0+△ M→M'切线转角为△ 定义 弧收预的华均商率为双A △O 曲线C在点M处的曲率为K=lim △S→0 △S △ 在lim 义=dC存在的条件下,K da △s-→0△S ds ds 2009年7月3日星期五 6 目录 上页 返回
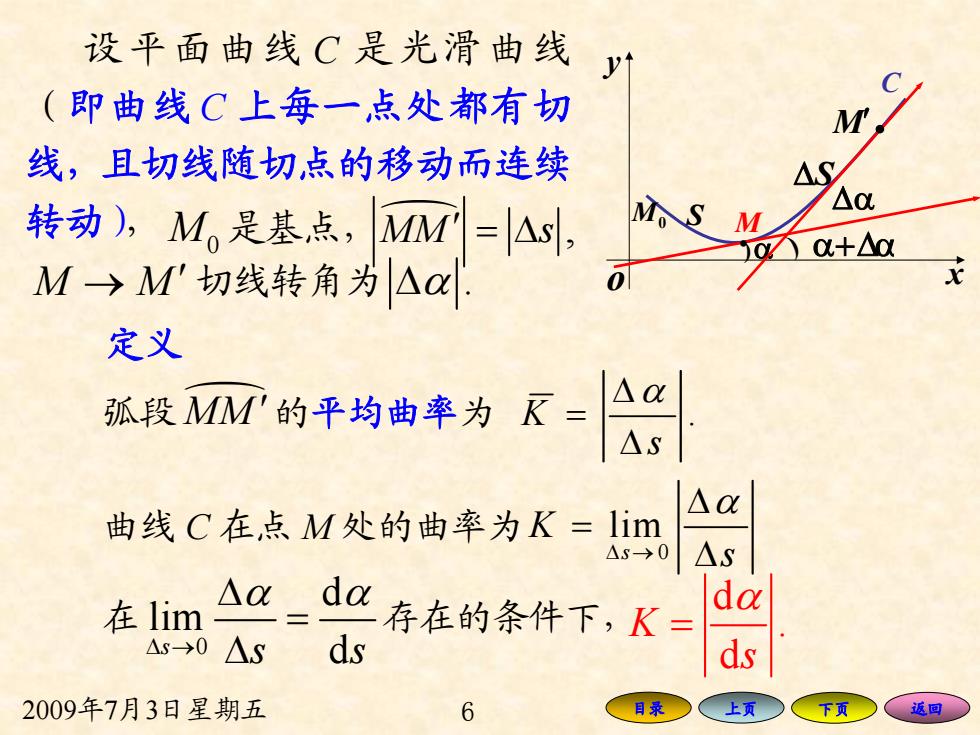
2009年7月3日星期五 6 目录 上页 下页 返回 设平面曲线 C 是光滑曲线 (即曲线 C 上每一点处都有切 线,且切线随切点的移动而连续 转动), y o x M C M0 M0 是基点, )α. M′. S ΔS M q M s ′ = Δ , M → M ′ 切线转角为 Δα . ) α+Δα Δα 定义 弧段M q M ′的平均曲率为 K . s Δα = Δ 曲线 C 在点 M 处的曲率为 0 lim s K s α Δ → Δ = Δ 在 0 d lim s s sd α α Δ → Δ = Δ 存在的条件下, d . d K sα =

例如,直线的曲率处处为零 事实上,△x=0,K= 又如,圆上各,点处的曲率等于半径的倒数,且半径越 小曲率越大 事实上, 设圆的半径为“,则由弧长、圆心角和半径的关系有 4a= △S 即4a 1 △S 故K= 2009年7月3日星期五 7 上页 返回
2009年7月3日星期五 7 目录 上页 下页 返回 事实上,Δ = α 0, 例如,直线的曲率处处为零. K 0 s Δα = = Δ 又如, 圆上各点处的曲率等于半径的倒数,且半径越 小曲率越大. 事实上, 设圆的半径为r ,则由弧长、圆心角和半径的关系有 s r α Δ Δ = 即 1 s r Δα = Δ 故 1 K s r Δα = = Δ