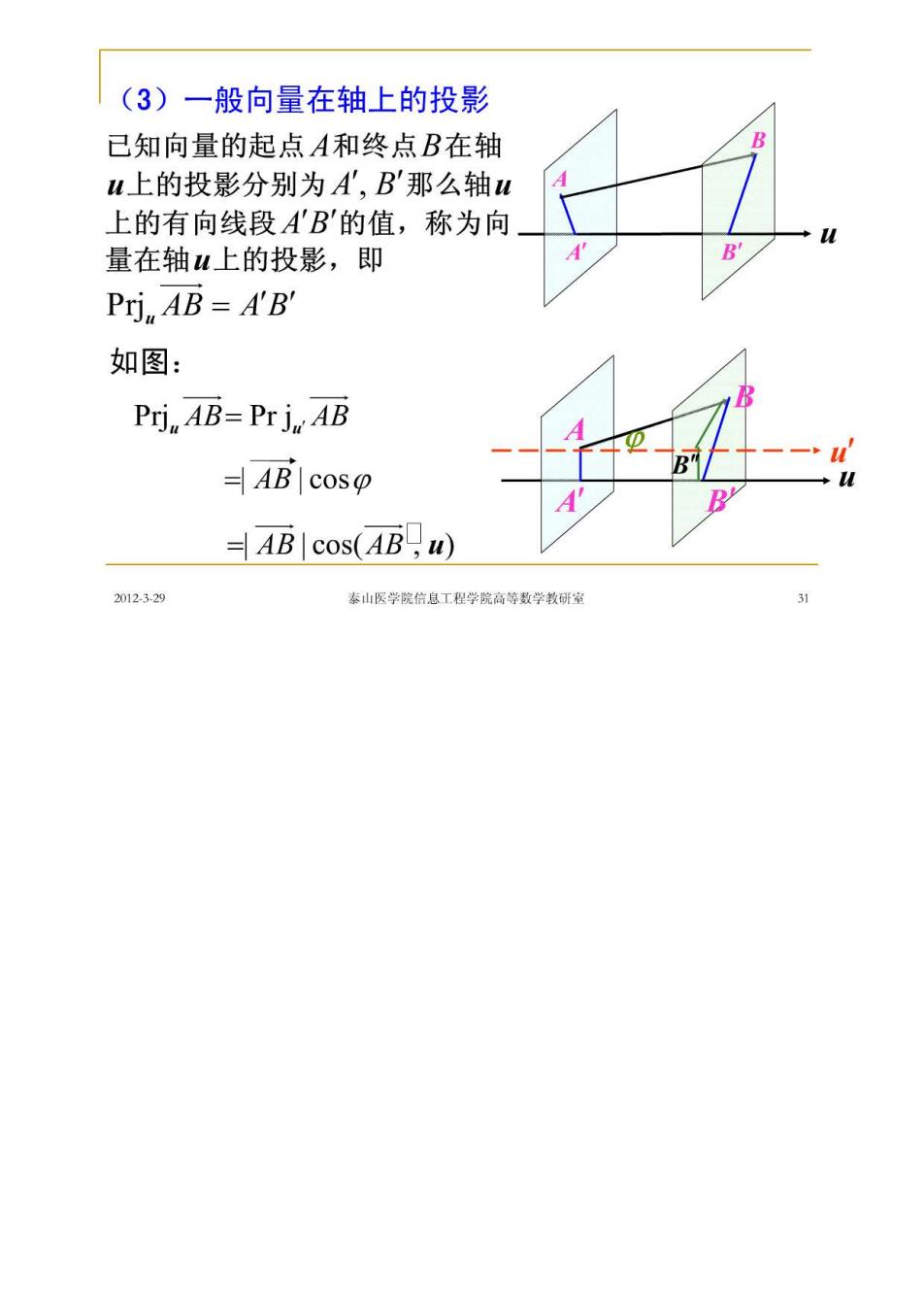
(3)一般向量在轴上的投影 已知向量的起点A和终点B在轴 M上的投影分别为A',B'那么轴u 上的有向线段AB的值,称为向 量在轴u上的投影,即 Prj,AB=A'B' 如图: Prj AB=Pr j AB 4B coso =AB|cos(AB,u) 2012329 泰山医学院信息工程学院高等数学教研室

(4)投影的性质 性质1 Prj,a=lalcosp,其中p为向量与u轴的夹角; 所以:向量a在直角坐标系中的坐标a,a,a,就是a在三条坐 标轴上的投影,即 a,=Prj,a,d,=Prj,a,a=Prj.a. 性质2 Prj(a+b)-Prja+Prjb; 性质3 Pri,(a)=APrj,a 2012329 泰山医学院信息工程学院高等数学教研室

例:设m=3i+5j+8k,n=2i-4j-7k, 币=5i+j-4K,求向量a=4m+3i-在x轴 上的投影及在y轴上的分向量. 解:a=4m+3n-元 =4(3i+5j+8R)+3(2i-4j-7k) -(5i+j-4k)=13i+7j+15k, ∴.在x轴上的投影为ax=13, 在y轴上的分向量为7j 2012329 泰山医学院信息工程学院高等数学教研室

六、小结 向量的概念 向量的加减法 向量与数的乘法(注意数乘向量的方向) 向量在坐标轴上的分向量与向量的坐标. (注意分向量与向量的坐标的区别) 向量的模与方向余弦的求法 向量在轴上的投影及其计算 2012329 泰山医学院信息工程学院高等数学教研室

第二节数量积向量积 一、两向量的数量积 二、两向量的向量积 2012-3-29 泰山医学院信息工程学院高等数学教研室 35