第七章多元函数微分法及其应用 一、知识结构图与学习要求 (一)知识结构图 多元函数、极限、连续的概念 -阶偏导数的概念及求法 偏导数 高阶偏导数的概念及求法 复合函数的求导公式 隐函数的求导公式 ”全微分的概念及求法 全微分 可微的条件 数 可微、偏导数存在、连续的关系 分法 全微分的形式不变性 「概念 方向导数与梯度计算方法 其应用 (两者的关系 空间曲线的切线与法平面 多元微分学的几何应用 空间曲面的切平面与法线 无条件极值 多元函数极值与最值 条件极值与Lagrange乘数法 最值 二元函数的Taylor公式 (二)学习要求 1.理解多元函数的概念,理解二元函数的几何意义. 2.了解二元函数的极限与连续性的概念,以及有界闭区域上连续函数的性质」
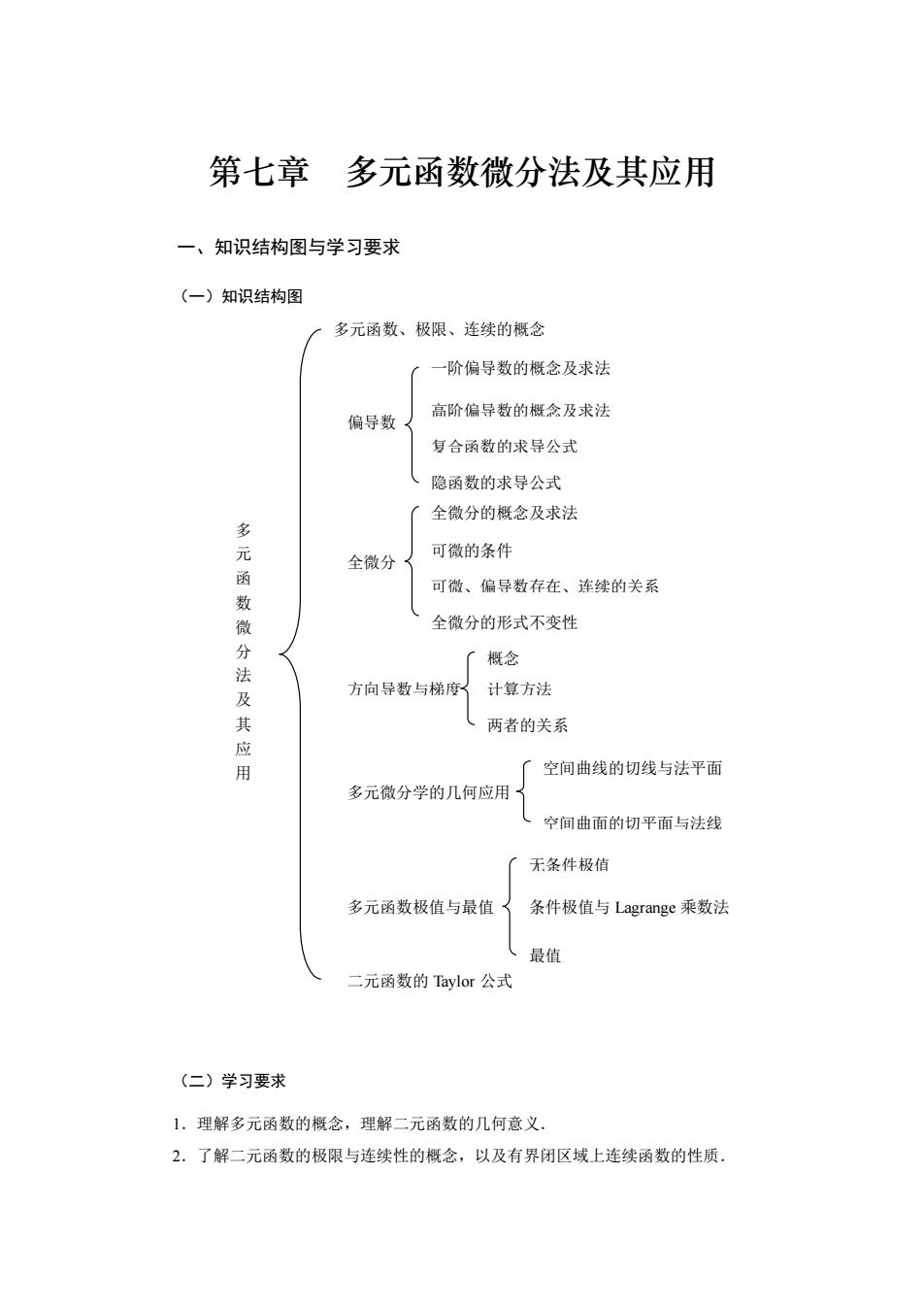
第七章 多元函数微分法及其应用 一、知识结构图与学习要求 (一)知识结构图 (二)学习要求 1.理解多元函数的概念,理解二元函数的几何意义. 2.了解二元函数的极限与连续性的概念,以及有界闭区域上连续函数的性质. 多 元 函 数 微 分 法 及 其 应 用 多元微分学的几何应用 空间曲线的切线与法平面 隐函数的求导公式 方向导数与梯度 一阶偏导数的概念及求法 偏导数 多元函数、极限、连续的概念 空间曲面的切平面与法线 复合函数的求导公式 概念 全微分 可微、偏导数存在、连续的关系 多元函数极值与最值 条件极值与 Lagrange 乘数法 无条件极值 全微分的概念及求法 高阶偏导数的概念及求法 可微的条件 全微分的形式不变性 二元函数的 Taylor 公式 计算方法 两者的关系 最值

3.理解多元函数偏导数和全微分的概念,会求全微分,了解全微分存在的必要条件和 充分条件,了解全微分形式的不变性。 4.理解方向导数与梯度的概念并掌握其计算方法 5.掌握多元复合函数一阶、二阶偏导数的求法」 6.了解隐函数存在定理,会求多元隐函数的偏导数. 7.了解空间曲线的切线和法平面及曲面的切平面和法线的概念,会求它们的方程。 8.了解二元函数的二阶泰勒公式. 9.理解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二 元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求 简单多元函数的最大值和最小值,并会解决一些简单的应用问题. 二、内容提要 (一)多元函数的极限与连续 1.二元函数的概念 设D是平面点集,如果对每个点P(x,y)ED,变量:按照一定的法则总有唯一确定的 值和它对应,则称:是变量x,y(或点P)的二元函数,记作:=x,)或:=fP) 称D是该函数的定义域。类似可以定义三元或三元以上的函数 2.二元函数的极限 设:=fx,)在区域D内有定义,(x%)是D的聚点,若存在常数A,使得 6>0,36>0,当P(x,y)∈DnU(P,)时, f(x,y)-A<s, 则称:=fx,)当P→B时以A为极限,记作 职在川=4或mfk以=4, 二元函数的极限也称为二重极限. 注二元函数极限的存在,等价于点P(x,)在fx,)的定义域中以任何方式趋于 B(:,%)时,x,)的极限都是A,由此可知,如果P(x,)沿某两种特殊方式趋于乃(化,) 时,f红)的极限不相同,则mx)不存在. 3.二元函数的连续性 设:=fx,)的定义域为D,B(,)为D的聚点,且B(,%)eD,如果 则称fx,)在P处连续,此时,D可以是开区域或闭区域,因此乃也可能是D的边界点.比 较一元连续函数在闭区间上的性质,二元连续函数在闭区域上也有类似的性质
3.理解多元函数偏导数和全微分的概念,会求全微分,了解全微分存在的必要条件和 充分条件,了解全微分形式的不变性. 4.理解方向导数与梯度的概念并掌握其计算方法. 5.掌握多元复合函数一阶、二阶偏导数的求法. 6.了解隐函数存在定理,会求多元隐函数的偏导数. 7.了解空间曲线的切线和法平面及曲面的切平面和法线的概念,会求它们的方程. 8.了解二元函数的二阶泰勒公式. 9.理解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二 元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求 简单多元函数的最大值和最小值,并会解决一些简单的应用问题. 二、内容提要 (一)多元函数的极限与连续 1.二元函数的概念 设 D 是平面点集,如果对每个点 P x y D ( , ) ,变量 z 按照一定的法则总有唯一确定的 值和它对应,则称 z 是变量 x , y (或点 P )的二元函数,记作 z f x y = ( , ) 或 z f P = ( ) 称 D 是该函数的定义域.类似可以定义三元或三元以上的函数. 2.二元函数的极限 设 z f x y = ( , ) 在区域 D 内有定义, 0 0 0 P x y ( , ) 是 D 的聚点,若存在常数 A ,使得 0, 0 ,当 0 P x y D U P ( , ) ( , ) 时, f x y A ( , ) − , 则称 z f x y = ( , ) 当 P P → 0 时以 A 为极限,记作 0 0 ( , ) ( , ) lim ( , ) x y x y f x y A → = 或 0 lim ( , ) P P f x y A → = , 二元函数的极限也称为二重极限. 注 二元函数极限的存在,等价于点 P x y ( , ) 在 f x y ( , ) 的定义域中以任何方式趋于 0 0 0 P x y ( , ) 时, f x y ( , ) 的极限都是 A,由此可知,如果 P x y ( , ) 沿某两种特殊方式趋于 0 0 0 P x y ( , ) 时, f x y ( , ) 的极限不相同,则 0 lim ( , ) P P f x y → 不存在. 3.二元函数的连续性 设 z f x y = ( , ) 的定义域为 D, 0 0 0 P x y ( , ) 为 D 的聚点,且 0 0 0 P x y D ( , ) ,如果 0 0 0 0 ( , ) ( , ) lim ( , ) ( , ) x y x y f x y f x y → = , 则称 f x y ( , ) 在 P0 处连续.此时,D 可以是开区域或闭区域,因此 P0 也可能是 D 的边界点.比 较一元连续函数在闭区间上的性质,二元连续函数在闭区域上也有类似的性质.

(二)偏导数与全微分 1.偏导数定义 如果 码+A-2 存在,则称此极限为函数:=fx,)在点乃(x,)处关于x的偏导数,记为 或鼠 6=画+4-f △y 为:=x,)在(x,为)处关于y的偏导数.在不引起混淆的情况下,有时为了记号的简单, 也将%)和f()记为x)和6). 由偏导数的定义可知,求偏导数实质上是求一元函数的导数的问题,如 0-孟 因此,一元函数的求导公式和求导法则对求偏导数也是适用的, 对三元或三元以上的多元函数亦可定义相应的偏导数. 2.偏导数几何意义 二元函数:=了化)在点(化,)的偏导数,)表示空间曲线r:任”在点 y=% M(不,fx乃》处的切线对x轴的斜率。 3.高阶偏导数 设话数:=化)在区城D内其有偶号数会小,年=,那么在D内 (x,(x,)都是(x,)的函数.如果这两个函数的偏导数也存在,则称它们为函数 :=(x,y)的二阶偏导数.按照对变量求导次序的不同有下列四个二阶偏导数 )-等-cm (器-: )点= 其中后边两个偏导数称为混合偏导数. 4.二阶混合偏导数相等的充分条件 如果函数的两个二阶混合偏号数需及器在区城口内莲续,影么在该区该内这两个
(二)偏导数与全微分 1.偏导数定义 如果 0 0 0 0 0 ( , ) ( , ) lim x f x x y f x y → x + − 存在,则称此极限为函数 z f x y = ( , ) 在点 0 0 0 P x y ( , ) 处关于 x 的偏导数,记为 0 0 0 0 ( , ), x P P f z f x y x x 或 . 称 0 0 0 0 0 0 0 ( , ) ( , ) y ( , ) lim y f x y y f x y f x y → y + − = 为 z f x y = ( , ) 在 0 0 0 P x y ( , ) 处关于 y 的偏导数.在不引起混淆的情况下,有时为了记号的简单, 也将 0 0 ( , ) x f x y 和 0 0 ( , ) y f x y 记为 1 0 0 f x y ( , ) 和 2 0 0 f x y ( , ) . 由偏导数的定义可知,求偏导数实质上是求一元函数的导数的问题,如 0 0 0 0 ( , ) ( , ) x x x d f x y f x y dx = = . 因此,一元函数的求导公式和求导法则对求偏导数也是适用的. 对三元或三元以上的多元函数亦可定义相应的偏导数. 2.偏导数几何意义 二元函数 z f x y = ( , ) 在点 0 0 ( , ) x y 的偏导数 0 0 ( , ) x f x y 表示空间曲线 0 ( , ) : z f x y y y = = 在点 0 0 0 0 M x y f x y ( , , ( , )) 处的切线对 x 轴的斜率. 3.高阶偏导数 设函数 z f x y = ( , ) 在区域 D 内具有偏导数 ( , ) x z f x y x = , ( , ) y z f x y y = ,那么在 D 内 ( , ) x f x y , ( , ) y f x y 都是 ( , ) x y 的函数.如果这两个函数的偏导数也存在,则称它们为函数 z f x y = ( , ) 的二阶偏导数.按照对变量求导次序的不同有下列四个二阶偏导数 2 2 ( , ) xx z z f x y x x x = = , 2 2 ( , ) yy z z f x y y y y = = , 2 ( , ) xy z z f x y y x x y = = , 2 ( , ) yx z z f x y x y y x = = , 其中后边两个偏导数称为混合偏导数. 4.二阶混合偏导数相等的充分条件 如果函数的两个二阶混合偏导数 2 z x y 及 2 z y x 在区域 D 内连续,那么在该区域内这两个

三价混合滨号数必相等,即需 5.全微分的定义 设:=f(xy)在区域D内有定义,(x,)∈eD,(x+△x,y+A)eD,若存在与△x,△y无 关的A和B,使 A=f(x+A.y+Ay)-f(x.y)=MAx+BAy+ap),p=y0. 则称∫x,)在(x,)处可微,且称止=AAx+BAy为∫x,)在(x,)处的全微分. 二元函数的可微性是一元函数的可微性的推广.若:=(x,y)在(x,y)处可微,则它在 (x)处连续。一元函数可微与可导等价,但二元函数可微和存在偏导数却没有这样的关 系。实际上,若fx)在(x,)处可微,则它在该点处的偏导数存在,且全微分为 但反之则不一定成立,比如本章例14. 6.判别函数可微通常有两种方法 方法1若:=fxy)在(x,)的某邻域中的偏导数f(x,y)和(x,y)存在,且f(x,y) 和(x,)在(x,)处连续,则fx)在(x,)处可微. 方法2首先求x,)和(x),如果 -+0. 其中 L=fx+△xy+A)-fx,),p=V△r2+Ay2, 则fx,)在(x,)处可微 在利用方法1来确定∫x,)的可微性时,通常根据多元初等函数的连续性可知x,) 有连续的偏导数.而适用于方法2的具体问题往往是考虑x,)在一些特殊点的可微性。 其中(x,y)和∫x,y)一般要用定义求得. (三)多元复合函数微分法 1.复合函数的一阶偏导数 设:=fu,)可微,u=x,y)和v=x,)存在偏导数,则:=几x,以,x,叨有如下 关于x和y的偏导数: =+Ya色_Yu+ 特别地,若u=x),v=x),则:=几x(x刃对x的导数为 会杂+安
二阶混合偏导数必相等,即 2 z x y = 2 z y x . 5.全微分的定义 设 z f x y = ( , ) 在区域 D 内有定义, ( , ) , ( , ) x y D x x y y D + + ,若存在与 x ,y 无 关的 A 和 B,使 = + + − = + + z f x y y f x y A x B y o ( , ) ( , ) ( ) , 2 2 = + → x y 0 , 则称 f x y ( , ) 在 ( , ) x y 处可微,且称 dz A x B y = + 为 f x y ( , ) 在 ( , ) x y 处的全微分. 二元函数的可微性是一元函数的可微性的推广.若 z f x y = ( , ) 在 ( , ) x y 处可微,则它在 ( , ) x y 处连续.一元函数可微与可导等价,但二元函数可微和存在偏导数却没有这样的关 系.实际上,若 f x y ( , ) 在 ( , ) x y 处可微,则它在该点处的偏导数存在,且全微分为 z z dz dx dy x y = + . 但反之则不一定成立,比如本章例 14. 6.判别函数可微通常有两种方法 方法 1 若 z f x y = ( , ) 在 ( , ) x y 的某邻域中的偏导数 ( , ) x f x y 和 ( , ) y f x y 存在,且 ( , ) x f x y 和 ( , ) y f x y 在 ( , ) x y 处连续,则 f x y ( , ) 在 ( , ) x y 处可微. 方法 2 首先求 ( , ) x f x y 和 ( , ) y f x y ,如果 0 [ ( , ) ( , ) ] lim 0 x y z f x y x f x y y → − + = , 其中 = + + − z f x x y y f x y ( , ) ( , ) , 2 2 = + x y , 则 f x y ( , ) 在 ( , ) x y 处可微. 在利用方法 1 来确定 f x y ( , ) 的可微性时,通常根据多元初等函数的连续性可知 f x y ( , ) 有连续的偏导数.而适用于方法 2 的具体问题往往是考虑 f x y ( , ) 在一些特殊点的可微性, 其中 ( , ) x f x y 和 ( , ) y f x y 一般要用定义求得. (三)多元复合函数微分法 1.复合函数的一阶偏导数 设 z f u v = ( , ) 可微, u u x y = ( , ) 和 v v x y = ( , ) 存在偏导数,则 z f u x y v x y = [ ( , ), ( , )] 有如下 关于 x 和 y 的偏导数: , z f u f v z f u f v x u x v x y u y v y = + = + . 特别地,若 u u x = ( ), v v x = ( ) ,则 z f u x v x = [ ( ), ( )] 对 x 的导数为 dz f du f dv dx u dx v dx = + .

称上述求导(或偏导)的公式为链式法则. 注这里要注意求偏导数的对象,即是对复合前的函数求导数(或偏导数),还是对复 合后的函数求偏导,例如 这里的表示复合前的二元函数:=化)关于x求偏导数,面失则表示复合以后的函数 =f化,(x》关于x求导数,二者切不可混为一谈. 2.一阶微分形式的不变性 设:=f(u,),u=x,y以,v=(x,)均可微,则无论将:=fu,)视为u、v的函数, 或视为x、y的函数,其微分相同,称之为一阶微分形式的不变性.该性质可用来求多元复 合函数的偏导数,而无需关注变量之间的关系, (四)隐函数的微分法 1.一个方程确定的隐函数 隐函数存在定理1设Fx,)在点P(x,%)的某一邻域内具有连续偏导数,且 Fx,)=0,F6)≠0,则方程F(x,)=0在点(化,)的某一邻域内恒能唯一确定 个连续且具有连续导数的函数y=x),它满足条件=(x),并有 dy F(x.) 若F(x,)有二阶连续偏导,则在相应条件下,有 0-2 隐函数存在定理2设函数F(x,y)点P(x,)的某一邻域内具有连续偏导数,且 F(x,)=0,F'(x,%,o)≠0,则方程F(x,y,)=0在点(30,)的某一邻域内恒能唯 一确定一个连续且具有连续偏导数的函数:=(x,),它满足条件。=x,),并有 正F(x aFx,y,) axE(x.v.)' ayF(x.y.=)' 2.方程组确定的隐函数 设方程组业丝二0确定隐函数“=(x以=x),记 J-0EGIF a可GGo, 则对方程组关于x和y求偏导数可得
称上述求导(或偏导)的公式为链式法则. 注 这里要注意求偏导数的对象,即是对复合前的函数求导数(或偏导数),还是对复 合后的函数求偏导,例如 z f x y x = ( , ( )) , dz f f dy dx x y dx = + , 这里的 f x 表示复合前的二元函数 z f x y = ( , ) 关于 x 求偏导数,而 dz dx 则表示复合以后的函数 z f x y x = ( , ( )) 关于 x 求导数,二者切不可混为一谈. 2.一阶微分形式的不变性 设 z f u v = ( , ),u u x y v v x y = = ( , ), ( , ) 均可微,则无论将 z f u v = ( , ) 视为 u 、v 的函数, 或视为 x 、y 的函数,其微分相同,称之为一阶微分形式的不变性.该性质可用来求多元复 合函数的偏导数,而无需关注变量之间的关系. (四)隐函数的微分法 1.一个方程确定的隐函数 隐函数存在定理 1 设 F x y ( , ) 在点 0 0 P x y ( , ) 的某一邻域内具有连续偏导数,且 0 0 F x y ( , ) 0 = , 0 0 ( , ) 0 F x y y ,则方程 F x y ( , ) 0 = 在点 0 0 ( , ) x y 的某一邻域内恒能唯一确定一 个连续且具有连续导数的函数 y y x = ( ) ,它满足条件 0 0 y f x = ( ) ,并有 ( , ) ( , ) x y dy F x y dx F x y = − . 若 F x y ( , ) 有二阶连续偏导,则在相应条件下,有 2 2 2 2 3 2 xx y xy x y yy x y d y F F F F F F F dx F − + = − . 隐函数存在定理 2 设函数 F x y z ( , , ) 点 0 0 0 P x y z ( , , ) 的某一邻域内具有连续偏导数,且 0 0 0 F x y z ( , , ) 0 = , 0 0 0 ( , , ) 0 F x y z z ,则方程 F x y z ( , , ) 0 = 在点 0 0 0 ( , , ) x y z 的某一邻域内恒能唯 一确定一个连续且具有连续偏导数的函数 z z x y = ( , ) ,它满足条件 0 0 0 z f x y = ( , ) ,并有 ( , , ) ( , , ) , ( , , ) ( , , ) x y z z z z F x y z F x y z x F x y z y F x y z = − = − . 2.方程组确定的隐函数 设方程组 ( , , , ) 0 ( , , , ) 0 F x y u v G x y u v = = 确定隐函数 u u x y v v x y = = ( , ), ( , ) ,记 ( , ) 0 ( , ) u v u v F G F F J u v G G = = , 则对方程组关于 x 和 y 求偏导数可得