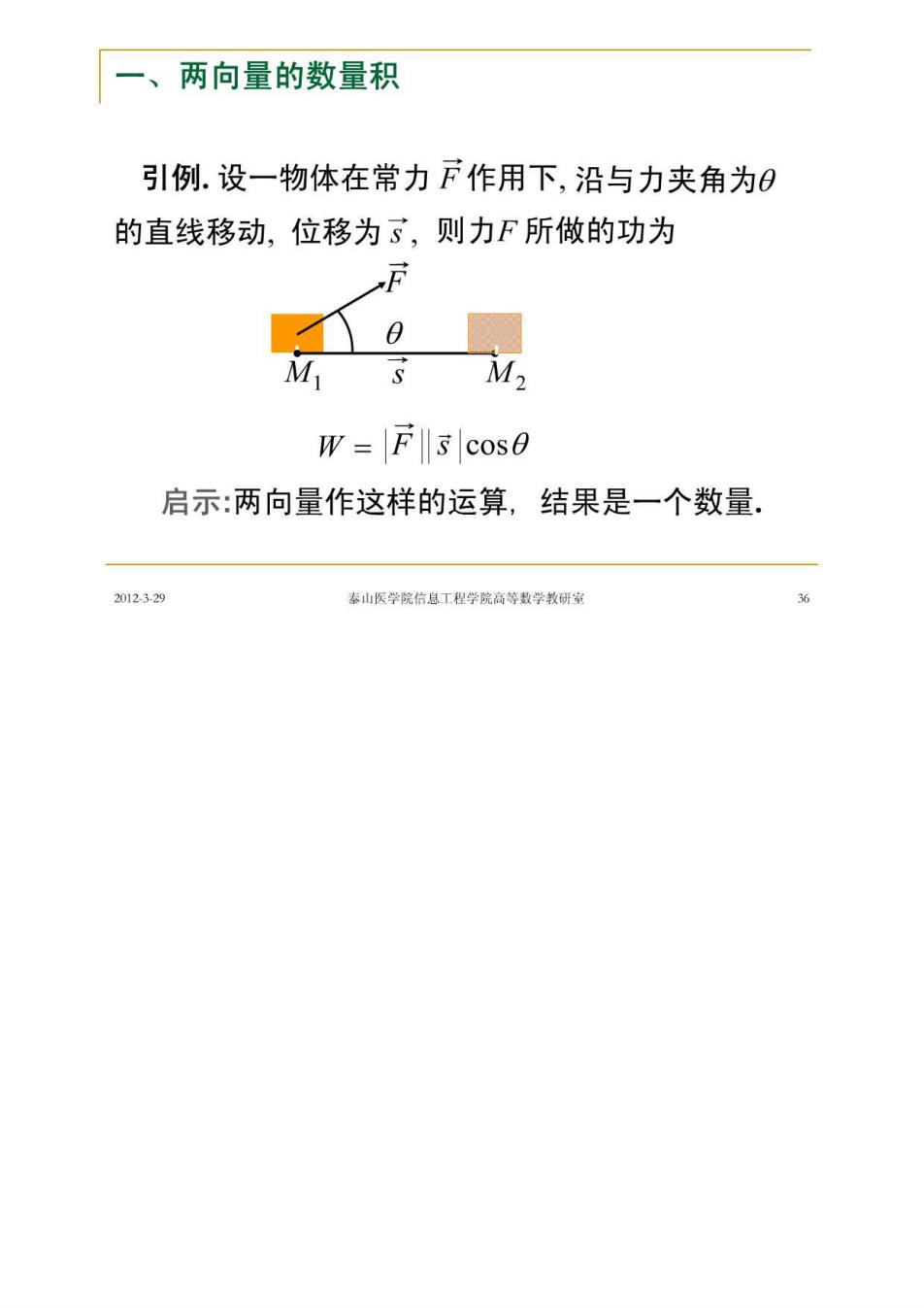
一、两向量的数量积 引例.设一物体在常力F作用下,沿与力夹角为0 的直线移动,位移为3,则力F所做的功为 M M W=F‖cos0 启示:两向量作这样的运算,结果是一个数量. 2012329 泰山医学院信息工程学院高等数学教研室

1.定义 设向量a,b的夹角为0,称 ab cos0= 记作a币 为a与b的数量积(点积). 【定义扩展】当ā≠0时,五在ā上的投影为 bcos0—Prjab 故 aB=a PriaB a 同理,当6≠0时, ab=bPrina 2012329 泰山医学院信息工程学院高等数学教研室

2.性质 ()a.a=a2 因为aa=aacos(0=a ii=jj=kk=可 (2)a,b为两个非零向量,则有 a.b=0三a⊥b, 证:(→)a.b=0,|a≠0,b≠0, cos0=0,0=a6. (台)a6,0=受c0s0=0 2012329 a.b=abc0s8版0

3.运算律 (1)交换律a.b=bd (2)结合律(几,4为实数) (a)-b=a(b)=2(a.b) (a+b) (2a)(ub)=(a(ub) =au(a.b) Prie a Prjeb (3)分配律(a+b)c=a·c+bc Prjz(a+b) 事实上,当c=0时,显然成立;当≠0时 (a+b)-c=cPrjz(a+b)=c|(Prje@+Prjeb) =C Prjea+c Prjeb=a.c+b.c 2012329 泰山医学院信息工程学院商等数学教研室

例1.证明三角形余弦定理 c2 =a2+b2-2abcos0 证:如图.设 CB=a,CA=b,AB=c 则 c-a-b B /0 IcP=(q-B)(G-B)-a.q+b.B-2a.B =laP+|3P-2allbcos0 a=a,b=b,c=c c2 =a2+b2-2abcos0 2012329 泰山医学院信息工程学院高等数学教研室