
2.方向角与方向余弦 (1)空间两向量的夹角: 1p i≠0,b≠0, a 向量a与向量6的夹角p=(a,b)=(⑦,a)(0≤p≤) 类似地,可定义向量与一轴或空间两轴的夹角. 特殊地,当两个向量中有一个零向量时,规定 它们的夹角可在0与元之间任意取值. (2)方向角与方向余弦: 给定F=(xy,z)≠0,称F B 与三坐标轴的夹角,B,y为其方向角。 2012329 泰山医学院信息工程学院高等数学教研室

方向角的余弦称为其方向余弦, x cosa 向+y+ COsB= y FVx2+y2+22 cosy= Fx2+y2+22 方向余弦的性质:cos2a+cos2B+cos2y=1 向量下的单位向量: °= 2012329 .e升

例7.已知两点M1(2,2,√2)和M2(1,3,0),计算向量 MM2的模、方向余弦和方向角 解:M1M2=(1-2,3-2,0-√2) =(-1,1,-2) M1M2=V-1)2+12+(-√2)2=2 1 cosa = 2 =2 cosy=-2 CosB=1 2 a-2π 3, B=π 3 4 2012329 (os%49s么9se

例8.设点A,向径OA与x轴y轴的夹角依次为?,平, 且OA=6,求点A的坐标. 解:已知a=号,B=年,则 cos2y=1-cos2a-cos2 B= 故cosy=±2于是 0A=0Aem=6(3,±(3,32,±3) 故点A的坐标为(3,3V2,3)或(3,3V2,-3) 2012329 cos2&+cos B+c0s¥=1
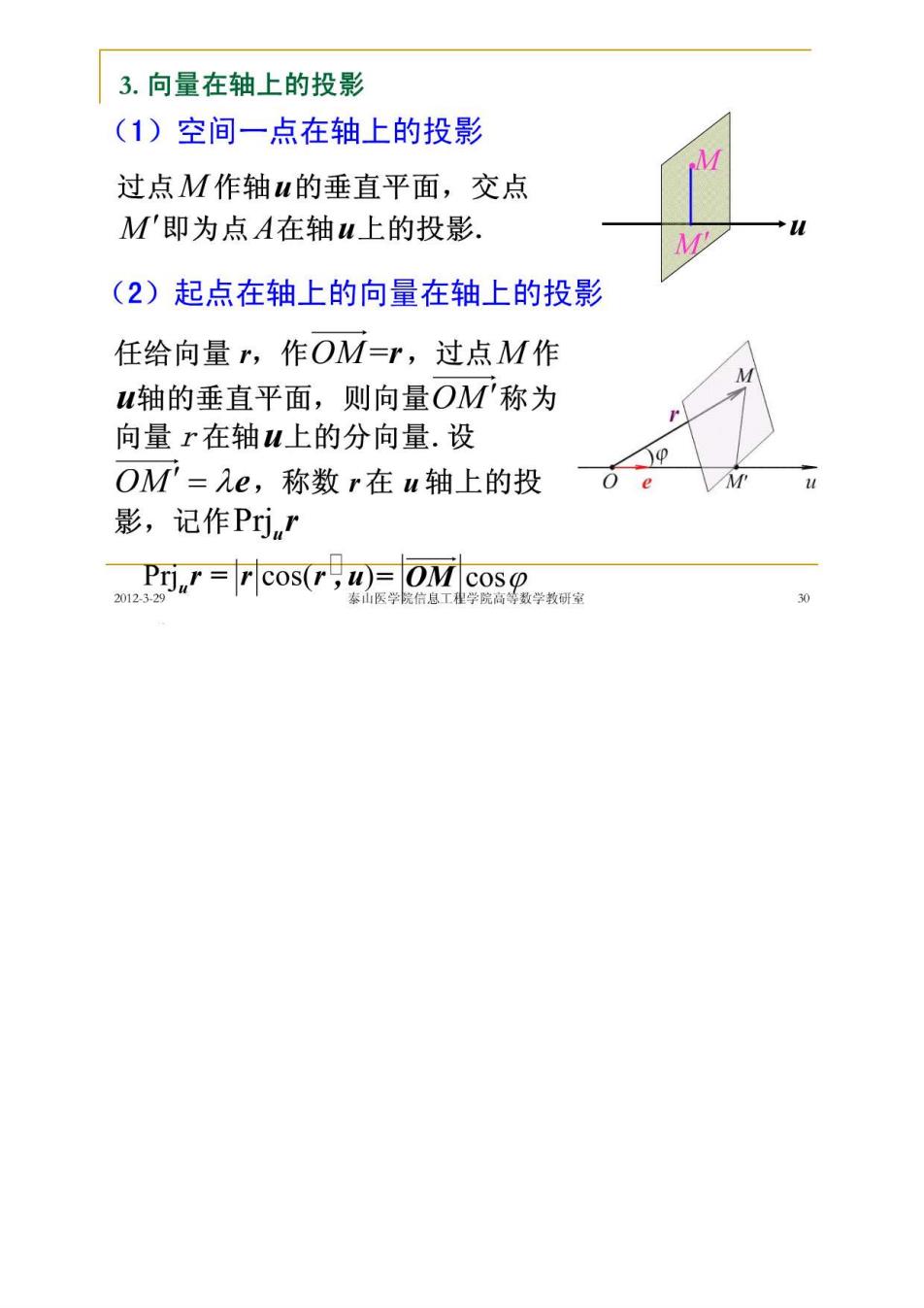
3.向量在轴上的投影 (1)空间一点在轴上的投影 过点M作轴u的垂直平面,交点 M'即为点A在轴u上的投影. M (2)起点在轴上的向量在轴上的投影 任给向量,作OM=r,过点M作 u轴的垂直平面,则向量OM'称为 向量r在轴u上的分向量.设 OM=e,称数r在u轴上的投 影,记作Prjr Pcos(oMcosg 院信恳工学院高数学教研