
第五章定积分 (Definite Integrals) 在一切理论成就中,未必再有什么象17世纪下半 叶微积分的发现那样被看作人类精神的最高胜利了。 如果在某个地方我们看到人类精神的纯粹的和唯一 的功绩,那也就是正是在这里。 恩格斯 2012329 素山医学院信息工程学院高等数学教研常

第一节 定积分的概念 (Concept of Definite Integrals) 问题的提出 二 定积分的定义 三四 定积分存在的两个充分条件 定积分的几何意义 五定积分的性质 六小结、思想方法 七思考题与判断题 2012-3-29 泰山医学院信息工程学院高等数学教研室 2

问题的提出(Introduction) 1 面积问题(Area Problem) 曲边梯形由连续曲线 y=f(x)(f(x)≥0)、 y=f(x) x轴与两条直线x=a、 A=? x=b所围成. 0 我们有两个问题要解决,一个是给出面积的定 义,一个是找出计算面积的方法。微积分的最大功 绩在于,用干净利索的方法解决了这一问题,并用 非常有效的方法解决了相当复杂的图形的面积的计 算问题。 2012.329 奉山医学院信息工程学院高等数学教研案 3
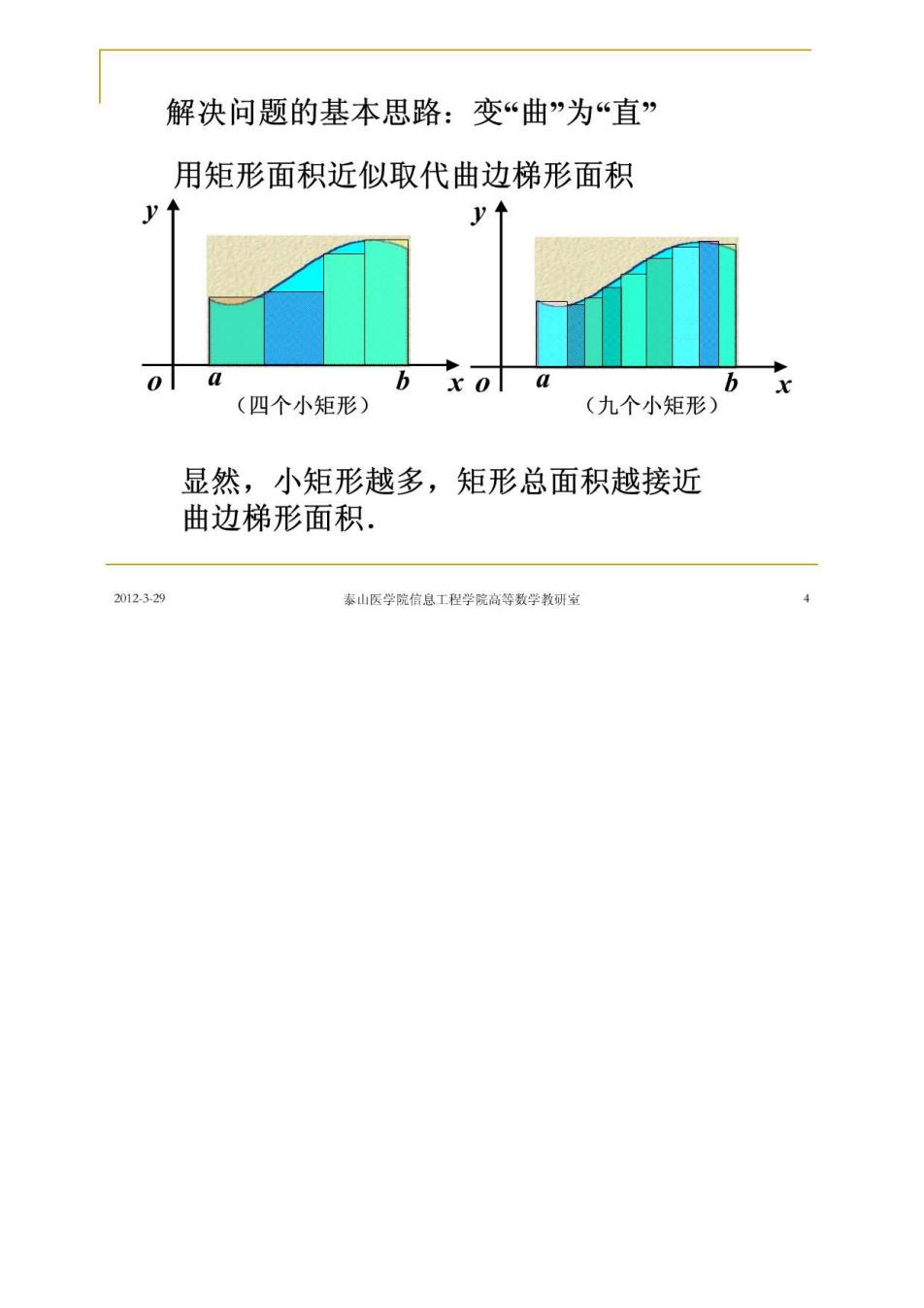
解决问题的基本思路:变“曲”为“直” 用矩形面积近似取代曲边梯形面积 xo a (四个小矩形) (九个小矩形)6 显然,小矩形越多,矩形总面积越接近 曲边梯形面积. 2012329 奉山医学院信息工程学院高等数学教研室
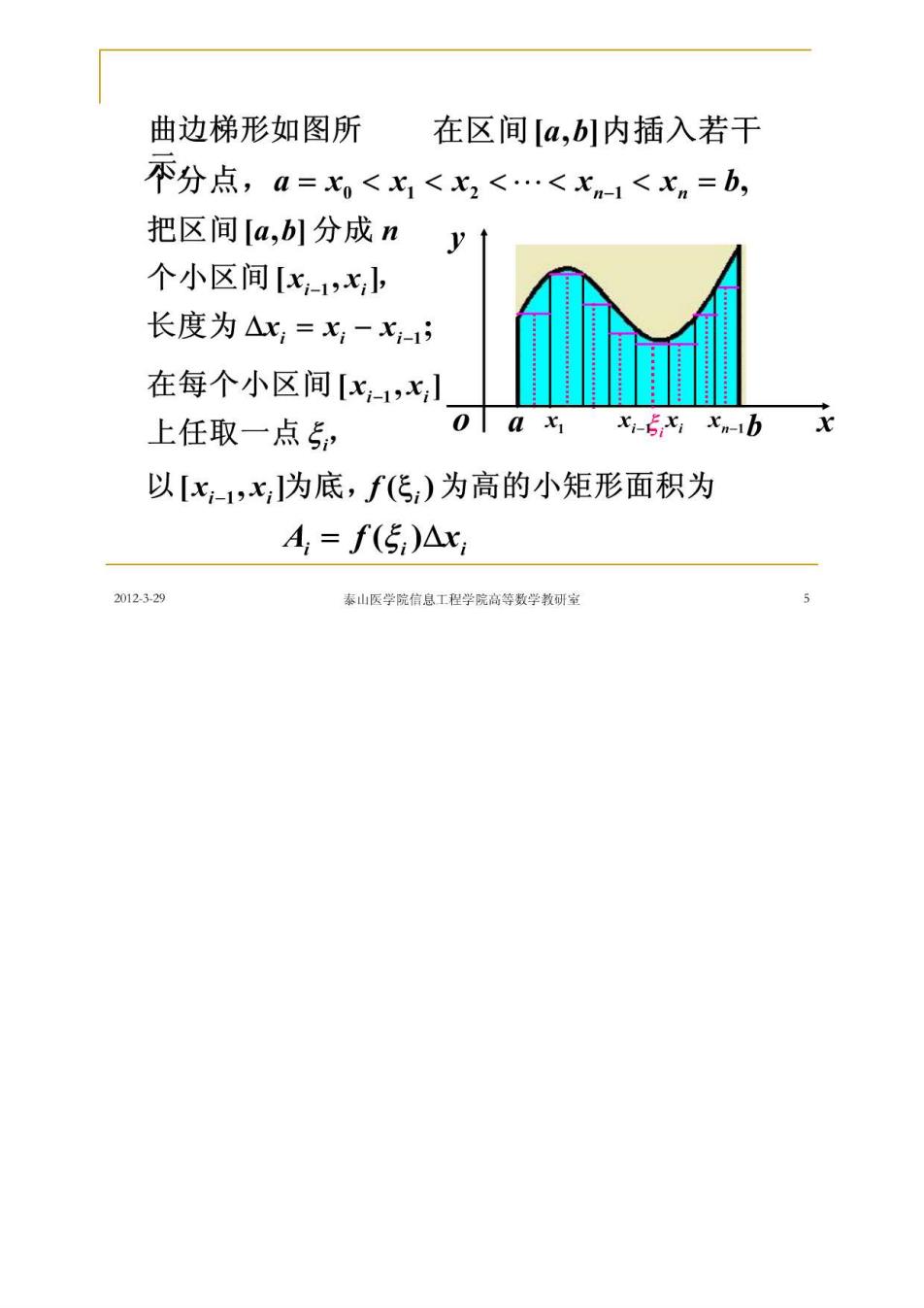
曲边梯形如图所 在区间[a,b]内插入若干 不分点,a=x<x1<x2<.<x1<xn=b, 把区间[a,b]分成n y 个小区间[x-1,x 长度为△x,=x-七- 在每个小区间[x1,x 上任取一点5, 0051x-5x,xm-1b 以[x1,x,为底,f(传)为高的小矩形面积为 A,=f(5)△x 2012329 素山医学院信息工程学院高等数学教研常