
第一节向量及其线性运算 一、空间直角坐标系 二、向量概念 三、向量的线性运算 四、利用坐标作向量的线性运算 五、向量的模、方向角、投影 2012-3-29 泰山医学院信息工程学院高等数学教研室 1
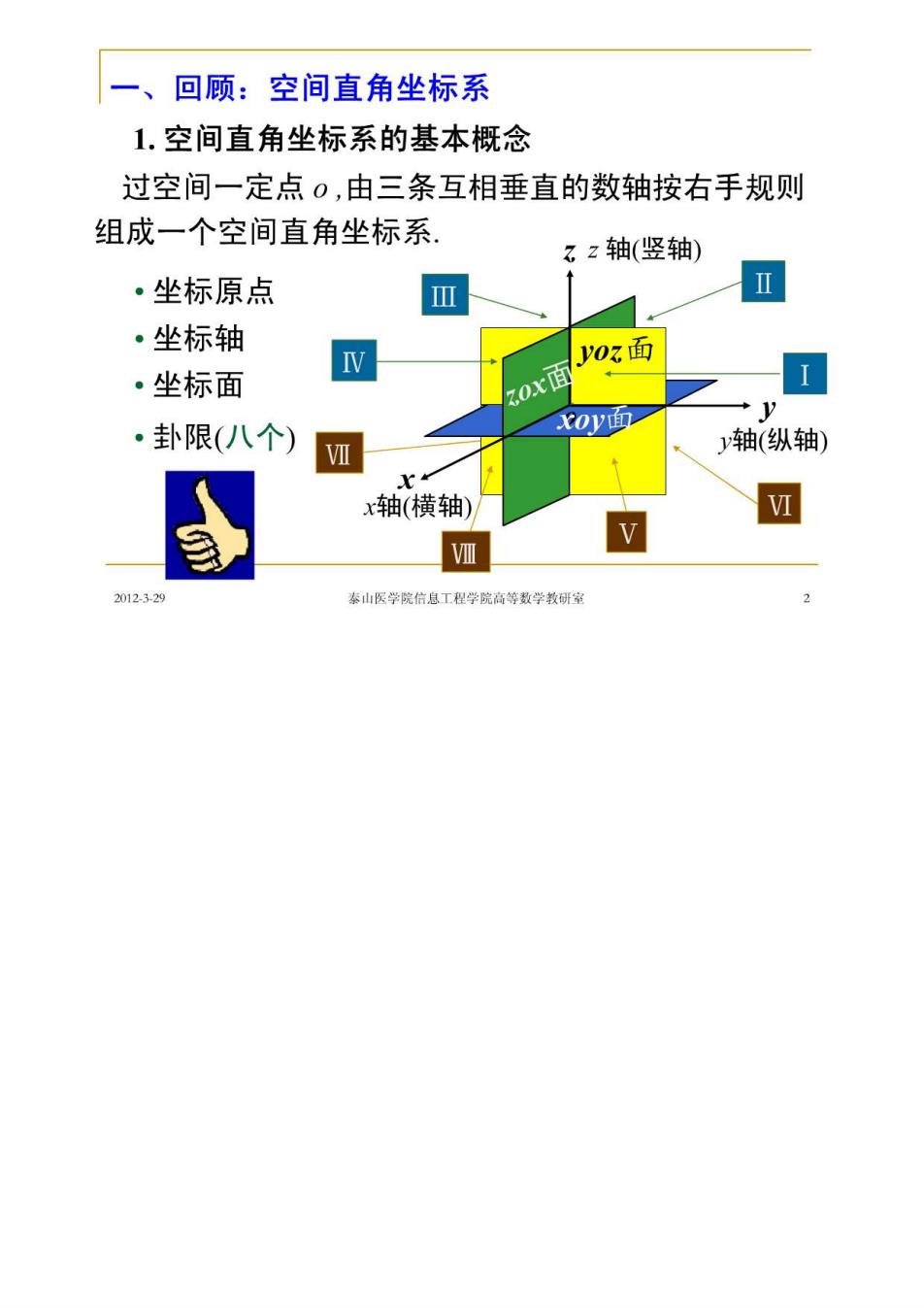
一、回顾:空间直角坐标系 1.空间直角坐标系的基本概念 过空间一定点0,由三条互相垂直的数轴按右手规则 组成一个空间直角坐标系, zz轴(竖轴) ·坐标原点 ·坐标轴 y0z面 ·坐标面 ·卦限(八个) x0y面 y轴(纵轴) 1 x轴(横轴) I 2012329 秦山医学院信息工程学院高等数学教研室

在直角坐标系下 点M←11→有序数组(化,y,z)(称为点M的坐标) 特殊点的坐标: 原点00,0,0); 坐标面上的点A,B,C R(0,0,z) B(0,y,z) C(x,0,z) 坐标轴上的点P,Q,R; Q(0,y,0) xP(x,0,0) A(x,y,0) 2012329 奉山医学院信息工程学院高等数学教研宝

两点间的距离公式: B A(1,Z)B(x2,y2,22), AB=Vx2-)2+0y-)2+(22-2)2 M(x,y,z) 0(0,0,0) 10M=x2+y2+z2 2012329 泰山医学院信息工程学院高等数学教研室

例1.求证以M1(4,3,1),M2(7,1,2),M3(5,2,3)为顶点 的三角形是等腰三角形. 证: M,M22=(7-42+1-3)2+(2-1)2=14 M,M,=(5-7)2+(2-1)2+(3-2)2=6 1M,M2=(5-4)2+(2-3)2+(3-102=6 ∴.M2M3=M1M3 M M 即△M1M2M3为等腰三角形 M2 2012329 泰山医学院信息工程学院高等数学教研室