
向量的单位化 设a*0,则向量“是与同方向的单位向量,记为e, a 按照向量与数的乘积的规定, a=he,一日=e 上式表明:一个非零向量除以它的模的结果是 一个与原向量同方向的单位向量 向量平行的充要条件 定理1设向量ā≠0,那么向量b平行于ā的充 分必要条件是:存在唯一的实数1,使b=2ā. 2012329 泰山医学院信息工程学院高等数学教研室

证明 条件的充分性显然;下证必要性 设5∥a取川-司 当6与ā同向时,1取正值, 当b与a反向时1取负值,即有i=a. 此时b与a同向. 且a=2a品团= 再证入的唯一性. 设万=1a,又设万=ua, 两式相减,得(2-)a=0,即2-4d=0, g同≠0,故240即怎4

四、利用坐标作向量的线性运算 1.向量的坐标表示 直线上点的坐标 点P一向量OP=xi一实数x 轴上点P的坐标为x的充分必要条件是OP=xi 平面上点的坐标 点M一向量OM=OP+PM =OP+00=xi+yj=(x,y) 轴上点M的坐标为(x,y)的充分 必要条件是OM=xi+y于 0 P 2012329 泰山医学院信息工程学院高等数学教研室
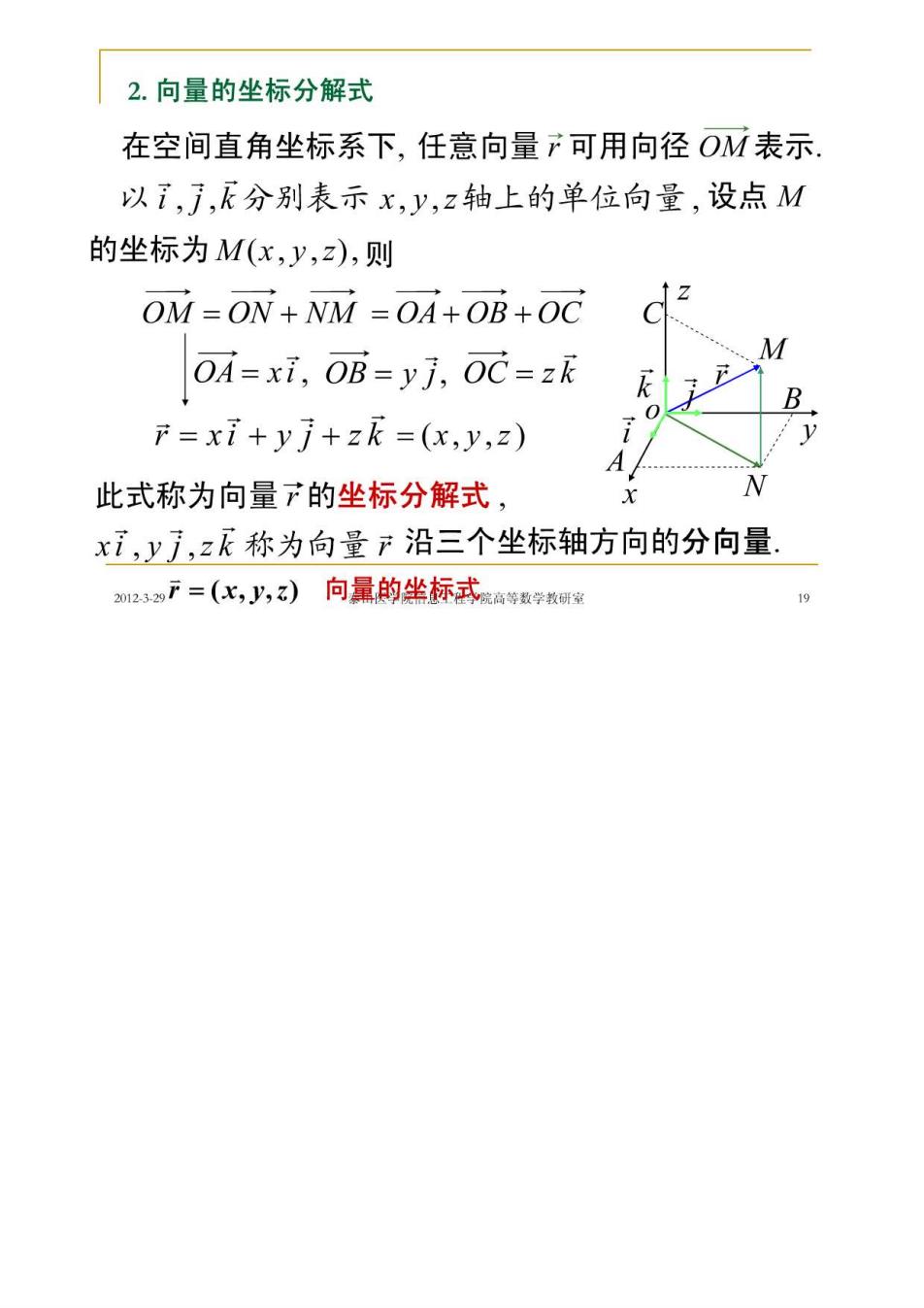
2.向量的坐标分解式 在空间直角坐标系下,任意向量F可用向径OM表示 以i,j,分别表示x,y,z轴上的单位向量,设点M 的坐标为M(x,y,z),则 OM=ON+NM =OA+0B+OC OA=xi,OB=yj,OC=zk F=xi+yj+zk=(x,y,z) 此式称为向量广的坐标分解式, x,y,z(称为向量产沿三个坐标轴方向的分向量. 别23F=(化,八,z)向量的坐标式商带数学教研家
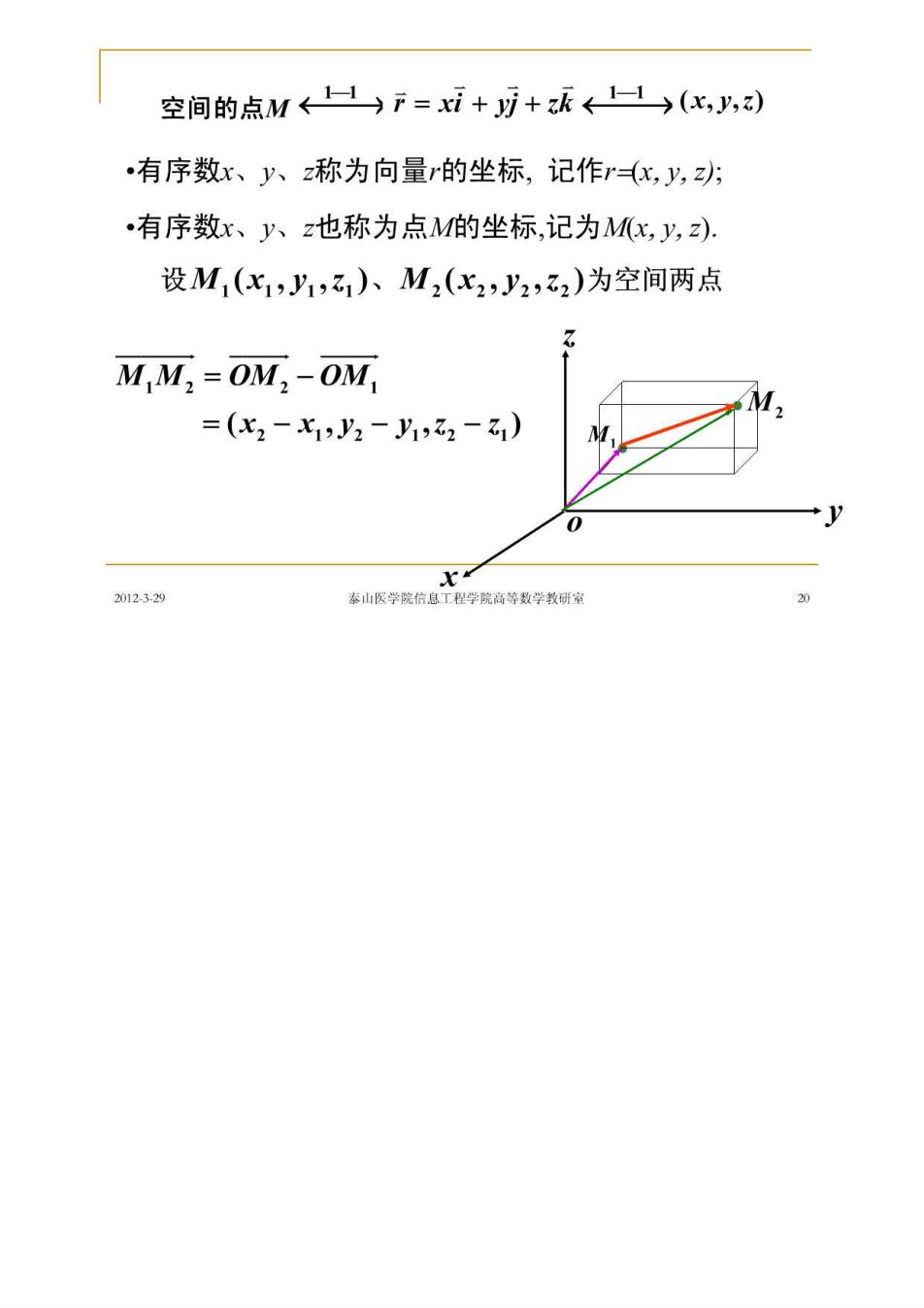
空间的点M←)F=xi+月+承←1(化,y,) ,有序数x、八、z称为向量的坐标,记作r化,y,功 ,有序数x、y八、z也称为点M的坐标,记为Mx,y,z) 设M1(x1,1,)、M2(x2,2,2)为空间两点 M,M,OM,-OM, =(x2-X1,2-y1,32-) 0 2012329 泰山医学院信恳工程学院高等数学教研室