
>例 (1) {《0,y川Jy∈R)一J轴上的点 (2){(x,y)川x>0,Jy>0}第一象限内的点 3){x,yx2+y2<1} _单位圆内的点 n维空间: 元有序实数组的全体构成的集合,即: {《K1,X2,xn)x,∈R,i=1,2,m记作:R"或R×RxxR n维空间中的元素: (化1,x2,xn)R"中的一个点或一个维向量 n维空间中的点集: R”中的任一子集
➢例 第一象限内的点 n维空间中的点集: 记作: (1) y轴上的点 (2) (3) 单位圆内的点 n维空间: n元有序实数组的全体构成的集合, 即: n维空间中的元素: {(0, y)| y R} {(x, y)| x 0, y 0} {( , )| 1} 2 2 x y x + y {( , , , )| , 1,2, , } x1 x2 xn xi R i = n R n 或 R R R ( , , , ) 1 2 n x x x R n 中的一个点或一个n维向量 R n 中的任一子集

多元函数的概念 (一)3引例 (二)平面点集 (三)多元函数的定义
一、多元函数的概念 (一)引例 (二)平面点集 (三)多元函数的定义

一、多元函数的概念 (一)3引例 (二)平面点集 (三)多元函数的定义
一、多元函数的概念 (一)引例 (二)平面点集 (三)多元函数的定义

>二元函数的定义 设D是R的一个非空子集,称映射f:D→R为定义在D上的 二元函数,记为 定义域 乙=f(x,y),(x,y)ED→ (D 因变量 自变量 值域 ●注 (1)二元函数也常记作乙=f(P),P∈D. (2)注意符号f和f化,y)的区别 (3)表示函数的记号可以任意选取 >元函数的定义 把二元函数定义中的平面点集D换成维空间R的点集D, 映射f:D→R就称为定义在D上的元函数
➢二元函数的定义 设D是 的一个非空子集, 2 R 称映射 为定义在D 上的 二元函数 , 记为 f ( D ) 因变量 自变量 定义域 值域 z = f (x, y),(x, y) D ⚫注 (2) 注意符号f 和f (x,y)的区别. (3) 表示函数的记号可以任意选取. (1) 二元函数也常记作: z = f (P), P D. ➢n元函数的定义 把二元函数定义中的平面点集D换成n维空间 的点集D, 映射f:D→R就称为定义在D上的n元函数. n R
>二元函数的图形 对于在z=xy)的定义域内任意取定的点P(化,y),对应的 函数值为=xy). 当(心y)遍取D上的一切点时,得到的空间点集 {x,y,)川z=f(x,y),(x,y)∈D 称为二元函数的图形 二元函数的图形通常是一张曲面. >二元函数的定义域 使算式有意义的点的集合 ◆例3求下列函数的定义域: (1)z=lmJy-x2)+V1-x2-y2(2)f(x,y)=1-x2
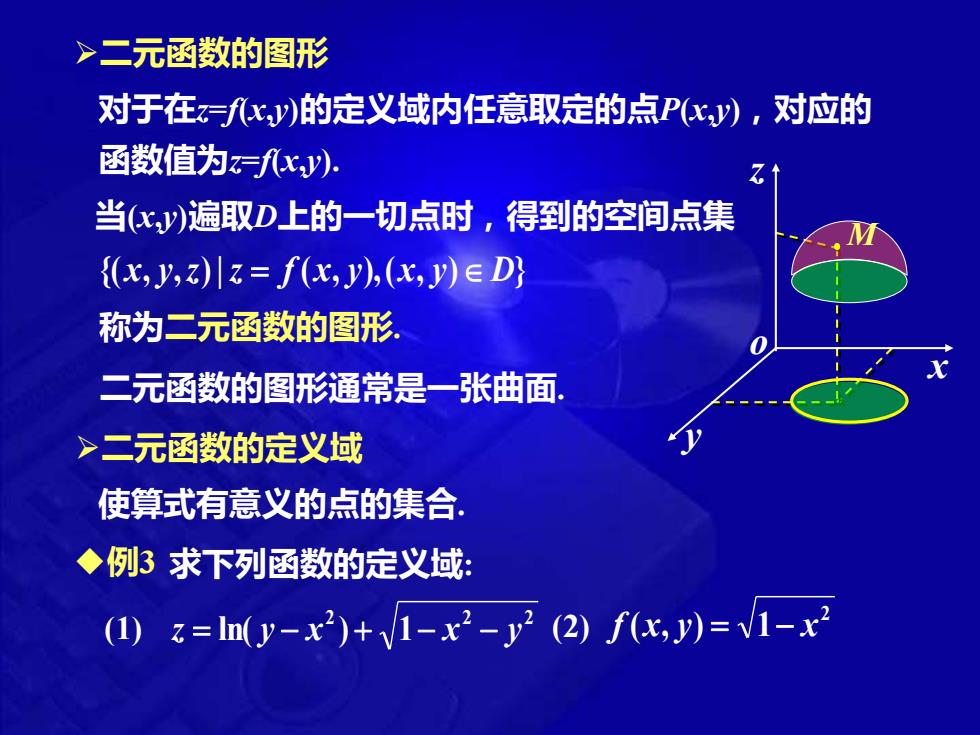
对于在z=f(x,y)的定义域内任意取定的点P(x,y),对应的 函数值为z=f(x,y). 当(x,y)遍取D上的一切点时,得到的空间点集 称为二元函数的图形. M 二元函数的图形通常是一张曲面. x o y z ➢二元函数的图形 {(x, y,z)| z = f (x, y),(x, y) D} ➢二元函数的定义域 使算式有意义的点的集合. ◆例3 求下列函数的定义域: (1) 2 2 2 z = ln( y − x ) + 1− x − y (2) 2 f (x, y) = 1− x