柱面 平行于定直线L并沿定曲线C移动的直线所成 的曲面,称为柱面,定曲线C称为柱面的准线, 动直线称为柱面的母线. L 涵 X
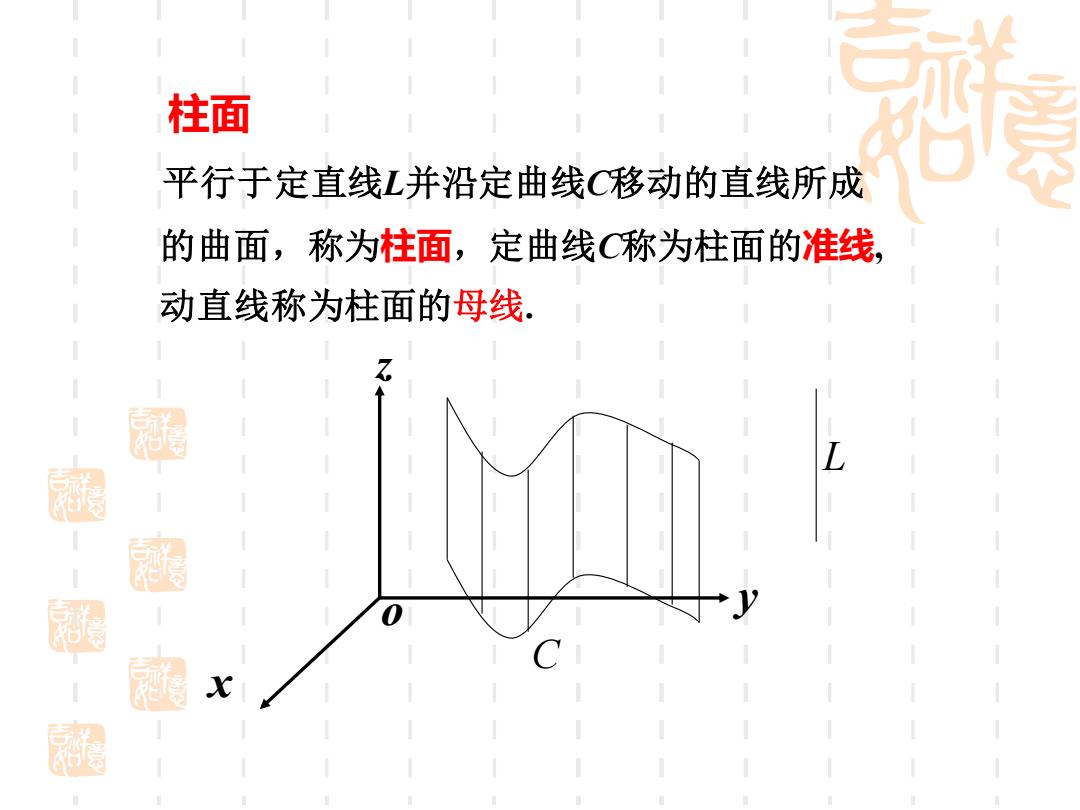
柱面 平行于定直线L并沿定曲线C移动的直线所成 x y z o L C 动直线称为柱面的母线. 的曲面,称为柱面,定曲线C称为柱面的准线

设柱面∑的母线平行于z轴,准线C是xy面上 的一条曲线,其方程为 「z=0 f(x,y)=0 可以证明:柱面Σ的方程是F(x,y)=0 从柱面方程看柱面的特征: 只含x,y而缺z的方程Fxy)=0,在空间直角坐标 系中表示母线平行于z轴的柱面,其准线为x0y 制 面上曲线C.(其他类推)
( , ) z f x y =0 =0 可以证明:柱面 的方程是 F x y ( , ) 0 = 设柱面 的母线平行于z 轴,准线C是 x y 面上 的一条曲线,其方程为 从柱面方程看柱面的特征: 只含x,y而缺z的方程F(x,y)=0,在空间直角坐标 系中表示母线平行于z轴的柱面,其准线为xoy 面上曲线C.(其他类推)

实例 2 y 2 B2 =1椭圆柱面优轴, a" =1双曲柱面/z轴, 湿 x2 2pi 抛物柱面y轴, -融私
1 2 2 2 2 + = c z b y 椭圆柱面 // x 轴, 1 2 2 2 2 − = b y a x 双曲柱面 // z 轴, x 2 pz 2 = 抛物柱面 // y 轴. 实例
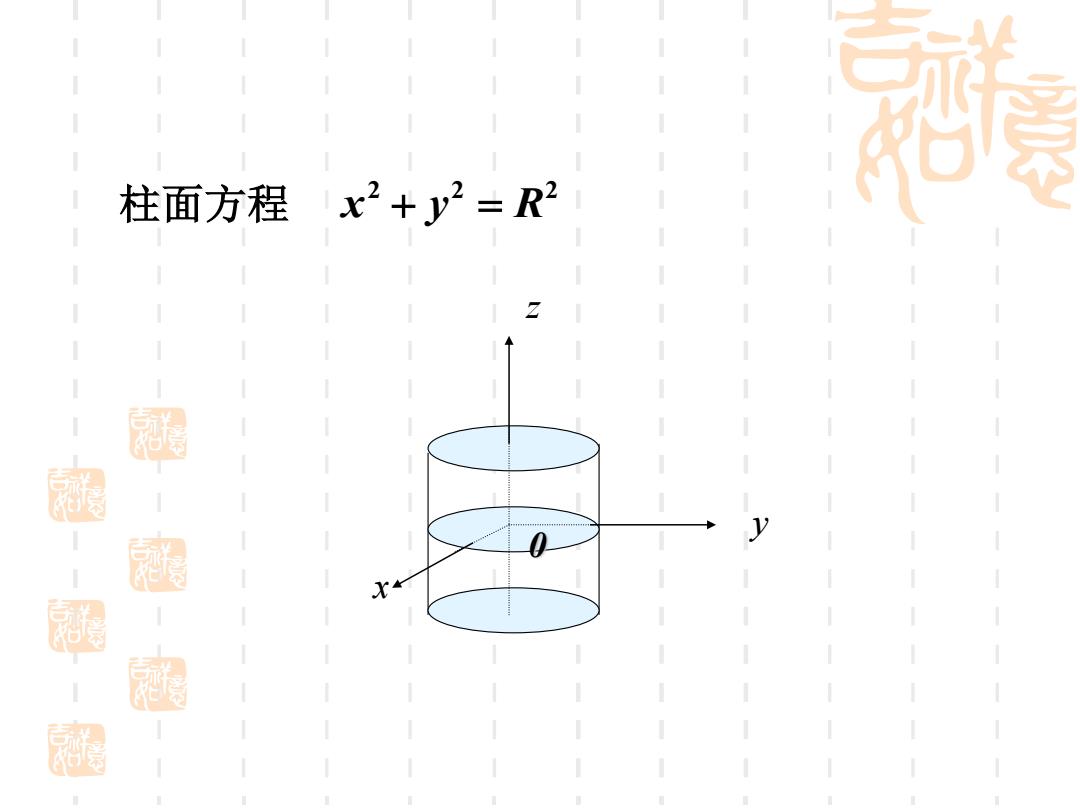
柱面方程x2+y2=R2 2
柱面方程 2 2 2 x + y = R x y z 0

二次曲面 二元二次方程所表示的曲面称为二次曲面 少例2求通过PK,)为中心,以R为半径的 球面S的方程. 解:设Px,y,)是球面S上的任一点,由球面的 刻 定义及两点间距离公式得 涵 Vx-x2+y-)2+(2-22=R (x-xo2+(y-)2+(z-2o2=R2 经过原点的球面的方程为:x2+y2十z2=R2
二次曲面 二元二次方程所表示的曲面称为二次曲面. 例2 解:设P(x,y,z) 是球面S上的任一点,由球面的 求通过P0 (x0 ,y0 ,z0 )为中心,以R为半径的 球面S的方程. 定义及两点间距离公式得 2 2 2 0 0 0 (x x y y z z R − − − = )+( )+( ) 2 2 2 2 0 0 0 (x x y y z z R − − − = )+( )+( ) . 经过原点的球面的方程为: 2 2 2 2 x y z R + + = . x y z o