
4.1.2空间两点间的距离 设P1化1y11),P2(K2y22)为空间任意两点.过P1 P,分别作平行于坐标平面的平面,这六个平面构成 一个以PP2为对角线的长方体,如下图所示,则其 三条边长分别为K1x2ly1y21z2,由勾股定理, 潮 得P与P2间的距离p为 -秋私 p=√x-+4-P+(2,-
4.1.2 空间两点间的距离 2 2 2 1 2 1 2 1 2 =(x x y y z z − − − )+( )+( ). 设P1 (x1 ,y1 ,z1 ) ,P2 (x2 ,y2 ,z2 )为空间任意两点.过P1 P2分别作平行于坐标平面的平面,这六个平面构成 一个以P1P2为对角线的长方体,如下图所示,则其 三条边长分别为|x1 -x2 |,|y1 -y2 |,|z1 -z2 |,由勾股定理, 得P1与P2间的距离ρ为
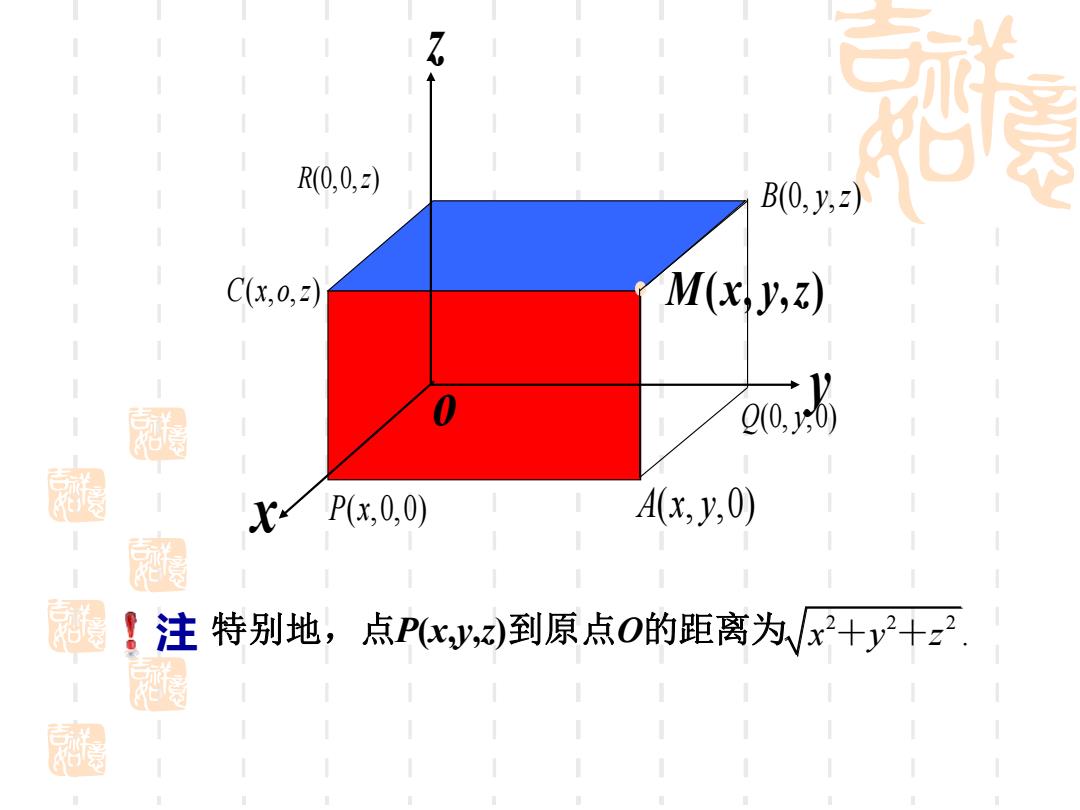
R0,0,z) B0,y,z) C(x,0,) M(x,y,) 通 XP(x,0,0) A(x,y,0) 漫 【注特别地,点PK,z)到原点O的距离为√x2+y2+z2
• M(x, y,z) x y z o P x( , 0, 0) Q y (0, , 0) R z (0, 0, ) A x y ( , , 0) B y z (0, , ) C x o z ( , , ) 注 特别地,点P(x,y,z)到原点O的距离为 2 2 2 x y z + +

少例1证明:以点M1(4,3,1),M2(7,1,3),M3 (5,2,3)为顶点的三角形是等腰三角形. 证明:由于 |MM,=4-5)+3-2)2+1-3)2=6 1M2M,=7-52+1-2)2+2-32=6, 所以,M,M=MM,=6. 潮 即△M1M2M3是等腰三角形
例1 证明: 由于 1 3 M M 4 5 3 2 1 3 6 − − − 2 =( )2 2 2 +( )+( )= , 2 3 M M 7 5 1 2 2 3 6 − − − 2 =( )2 2 2 +( )+( )= , 1 3 2 3 M M M M = = 6. 证明:以点M1 (4,3,1), M2 (7,1,3), M3 即△M1 M2 M3 是等腰三角形. 所以, (5,2,3)为顶点的三角形是等腰三角形

4.1.3 常见的空间曲面 如果曲面S与方程FK,y,z)=0之间存在这样的关系: (1)若点Mx,y,z)在曲面S上,则点M的坐标 M比,y,z)满足三元方程F化,y,z=0. (2) 若一组数x,,z满足方程F化,y,)=0,则点 湿 MK,y,z)就在曲面S上 称方程F化,,z)=O为曲面S的方程。 曲面S叫做方程F化,y,z)=0的图形
4.1.3 常见的空间曲面 如果曲面S与方程F(x, y, z)=0之间存在这样的关系: (1)若点M(x, y, z)在曲面S上,则点M的坐标 (2)若一组数x, y, z满足方程F(x, y, z)=0,则点 M(x, y, z)满足三元方程F(x, y, z)=0. M(x, y, z)就在曲面S上. 称方程F(x, y, z)=0为曲面 S的方程。 曲面S 叫做方程F(x, y, z)=0 的图形

【注空间的曲线可以看作是两个曲面的交线, 因此空间曲线的方程通常可以表示为: F(xy,z)=0 F(x,y,z)=0 湿 平面的方程Ax+By+Cz+D=O
注 空间的曲线可以看作是两个曲面的交线, 2 ( , , ) 0 . ( , , ) 0 F x y z F x y z = = 1 因此空间曲线的方程通常可以表示为: 平面的方程 Ax By Cz D + + + = 0