
第一节映射与函数记为fog,即(fog)(x)=flg(x)l.与复合映射一样,g与f能构成复合函数fg的条件是:函数g的值域R,必须包含于函数f的定义域D.,即R,CD.否则,不能构成复合函数.例如,y=f(u)=arcsinu的定义域为[-1,1l,u=g(x)=sinx的定义域为R,且g(R)C[-1,11故g与可构成复合函数,y=arcsin sin x,xeR;又如,y=f(u)=/u的定义域为D,=[0,+)u=g(x)=tanx的值域为R=(-0,+),显然R+D.故g与f不能构成复合函数.但是,如果将函数g限制在它的定义域的一个子集D=[xlk≤x<(h+2),kez|上,令g(x)=tanx,xeD,那么R。.=g(D)CD,g与f就可以构成复合函数(fog)(x)=Vtanx,xeD.习惯上为了简便起见,仍称函数tanx是由函数u=tanx与函数y=u构成的复合函数,这里函数u=tanx应理解成:u=tanx,xeD.以后,我们采取这种习惯说法.例如,我们称函数u=x+1与函数y=lnu构成复合函数ln(x+1),它的定义域不是u=x+1的自然定义域R,而是R的一个子集D=(-1,+),有时,也会遇到两个以上函数所构成的复合函数,只要它们顺次满足构成复o号这可构成复合函数y=合函数的条件.例如,函数y=/u,u=cotu,u=2里u及都是中间变量,复合函数的定义域是D=/x12kπ<x≤(2k+1)T,keZl,而不是=~的自然定义域R,D是R的一个非空子集,24.函数的运算设函数f),g()的定义域依次为D,D,D=D,nD→,则我们可以定义这两个函数的下列运算:和(差)f+g:(f±g)(x)=f(x)±g(x),xeD;积f·g:(f.g)(x)=f(x)-g(x),xED:商人白(x)=()g(eDV/xlg(x)=0, eD).g例11设函数f(x)的定义域为(-l,1),证明必存在(-1,I)上的偶函数g()及奇函数h(x),使得f(x)=g(x)+h(x)..11

第一章函数与极限证先分析如下:假若这样的g(x),h(x)存在,使得f(x)=g(x)+h(x),(1-1)且g(-x)=g(x),h(-x)=-h(x).于是有(1-2)f(-x)=g(-x)+h(-x)=g(x)-h(x)利用(1-1)、(1-2)式,就可作出g(x),h(x).这就启发我们作如下证明:作g(x)=[(x)+(-x) ],h(#)=[(×)-{(-x)].则g(x)+h(x)=f(x)g(-x)=→[(-x) f(x) ] =g(x),2(-x)-(x) =-h(x),h(-x)=-2证毕.5.初等函数在初等数学中已经讲过下面几类函数:幂函数:y=x(μeR是常数),指数函数:y=a*(a>0且a≠1)对数函数:y=logax(a>0且a手1,特别当a=e①时,记为y=lnx),三角函数:如y=sinx,y=cosx,y=tanx等,反三角函数:如y=arcsinx,y=arccosx,y=arctanx等以上这五类函数统称为基本初等函数由常数和基本初等函数经过有限次的四则运算和有限次的函数复合步骤所构成并可用一个式子表示的函数,称为初等函数.例如/cotty=/l-xy=sin'x,y:2等都是初等函数.在本课程中所讨论的函数绝大多数都是初等函数,应用上常遇到以e为底的指数函数y=e和y=e所产生的双曲函数以及它们的反函数—一反双曲函数.它们的定义如下:①e是一个无理数,这个数的意义见本章第六节。: 12 :
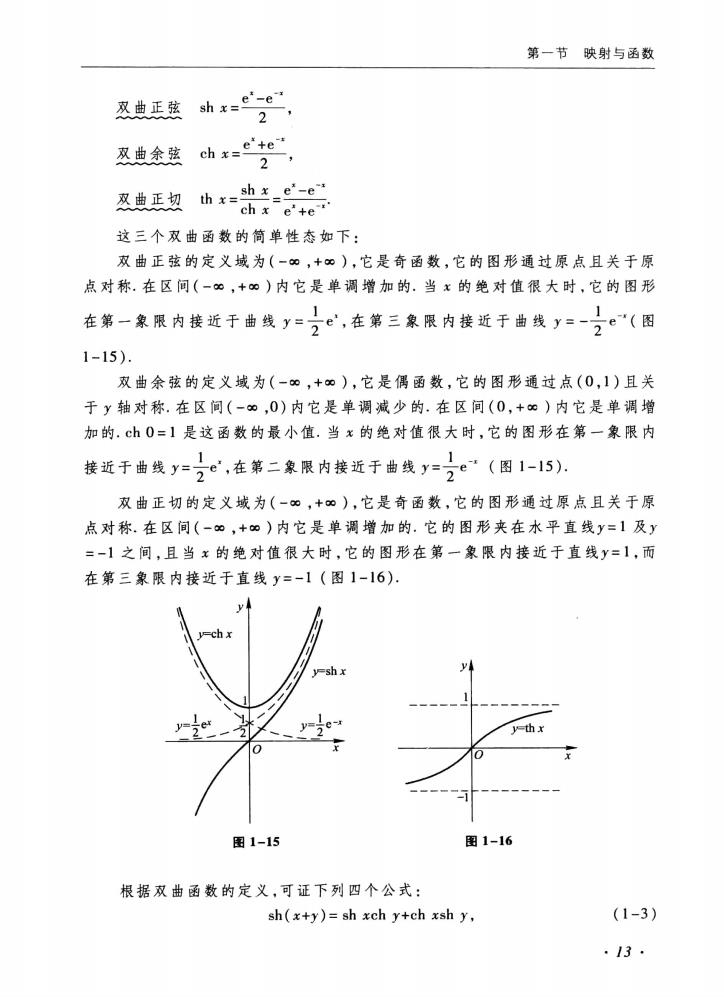
第一节映射与函数e"-esh x:双曲正弦2e'te"tch x=双曲余弦2,sh xe'-e"双曲正切th x:chx"e'+e这三个双曲函数的简单性态如下:双曲正弦的定义域为(一8,+8),它是奇函数,它的图形通过原点且关于原点对称.在区间(一,+)内它是单调增加的.当x的绝对值很大时,它的图形11e,在第三象限内接近于曲线y=在第一象限内接近于曲线y=e(图221-15).双曲余弦的定义域为(-,+),它是偶函数,它的图形通过点(0,1)且关于y轴对称.在区间(-0)内它是单调减少的在区间(0,+α)内它是单调增加的ch0=1是这函数的最小值.当x的绝对值很大时,它的图形在第一象限内一。,在第二象限内接近于曲线=1(图1-15).接近于曲线y=22双曲正切的定义域为(一,+),它是奇函数,它的图形通过原点且关于原点对称,在区间(-8,+)内它是单调增加的:它的图形夹在水平直线y=1及y=-1之间,且当x的绝对值很大时,它的图形在第一象限内接近于直线y=1,而在第三象限内接近于直线y=-1(图1-16)y4-ch xyAy-sh xy-thxX0x0图1-16图1-15根据双曲函数的定义,可证下列四个公式:(1-3)sh(x+y)= sh xch y+ch xsh y,:13

第一章函数与极限sh(x-y)= sh xch y-ch xsh y,(1-4)(1-5)ch(x+y)=chxch y+sh xshy,ch(x-y)= ch xch y-sh xsh y.(1-6)我们来证明公式(1-3),其他三个公式读者可自行证明由定义,得sh xch y+ch xsh ye'-e"e'+eye"+e"re-e"2222++e-*-e*-y-e-(++y)-(aty)+-ee-e44e**y-e-(a+)=sh(x+y).2由以上几个公式可以导出其他一些公式,例如:在公式(1-6)中令x=Y.并注意到ch0=1,得ch"x-sh"x=1;(1-7)在公式(1-3)中令x=y,得(1-8)sh 2x=2sh xch x;在公式(1-5)中令x=y,得ch 2x=ch"x+shx(1-9)以上关于双曲函数的公式(1-3)至(1-9)与三角函数的有关公式相类似,把它们对比可帮助记忆双曲函数y=shx,y=chx(x≥o),y=thx的反函数依次记为反双曲正弦y=arshx,反双曲余弦y=archx,反双曲正切y=arthx.这些反双曲函数都可通过自然对数函数来表示,分别讨论如下:先讨论双曲正弦y=shx的反函数由x=shy,有e"-e""2令u=e,则由上式有u2-2xu-1=0.这是关于u的一个二次方程,它的根为u=x±+.因u=e>0,故上式根号前应取正号,于是u=x+y+1.-14

第一节日映射与函数由于y=lnu,故得反双曲正弦y=arshx=ln(x+x+1)函数y=arshx的定义域为(-8,+),它是奇函数,在区间(-80,+)内为单调增加,由y=shx的图形,根据反函数的作图法,可得y=arshx的图形如图1-17所示,下面讨论双曲余弦y=chx(x≥0)的反函数y4y=arshx由x=chy(y≥0),有e'+e"2,≥0.Y-xO由此得e=x+/-1故y=ln(x±/-1).图1-17上式中x的值必须满足条件≥1,而其中平方根前的符号由于y≥0应取正:故y=ln(x+/2-1)上述双曲余弦y=chx(x≥0)的反函数称为反双曲余弦的主值,记作y=archx即y=archx=ln(x+/-1)这样规定的函数y=archx的定义域为[1,+o),它在区间[1,+)上是单调增加的(图1-18)类似地,可得反双曲正切11+xy=arth x=-In21-x这函数的定义域为开区间(-11),它在开区间(-1,1)内是单调增加的奇函数它的图形关于原点对称(图1-19)yly=arthxy=archx0x11-1!xo图1-19图1-18.15-