
复变函数2)可去奇点的判定(I)由定义判断:如果 f(z)在z。的洛朗级数无负幂项则 z为 f(z)的可去奇点(2)判断极限lim f(z):若极限存在且为有限值,Z→Z0则 z为 f(z)的可去奇点U
6 2) 可去奇点的判定 (1) 由定义判断: 如果 f (z) 在 z0 的洛朗级数无负 幂项则 0 z 为 f (z) 的可去奇点. (2) 判断极限 lim ( ): 0 f z z→z 若极限存在且为有限值, 则 0 z 为 f (z) 的可去奇点

复变函数sin z21例31中不含负幂项...17十73!5!Zsin z是z =0的可去奇点·7如果补充定义:sin zz=0时,= 1,zsin z那末在 z=0解析7u
7 如果补充定义: z = 0 时, 1, sin = z z 那末 z sin z 在 z = 0 解析. 例3 = − 2 + 4 − 5! 1 3! 1 1 sin z z z z 中不含负幂项, z = 0 是 z sin z 的可去奇点
复变函数e例4 说明z=0为的可去奇点。Zez-12解(1z"+...-1)++7一-2!n!Z7一n-120z+8++....-Z+...7+2!n!无负幂项ez-1所以 z=0为的可去奇点7ez-1因为另解lime" = 1,limz-0z-→0N一e所以 =为的可去奇点U
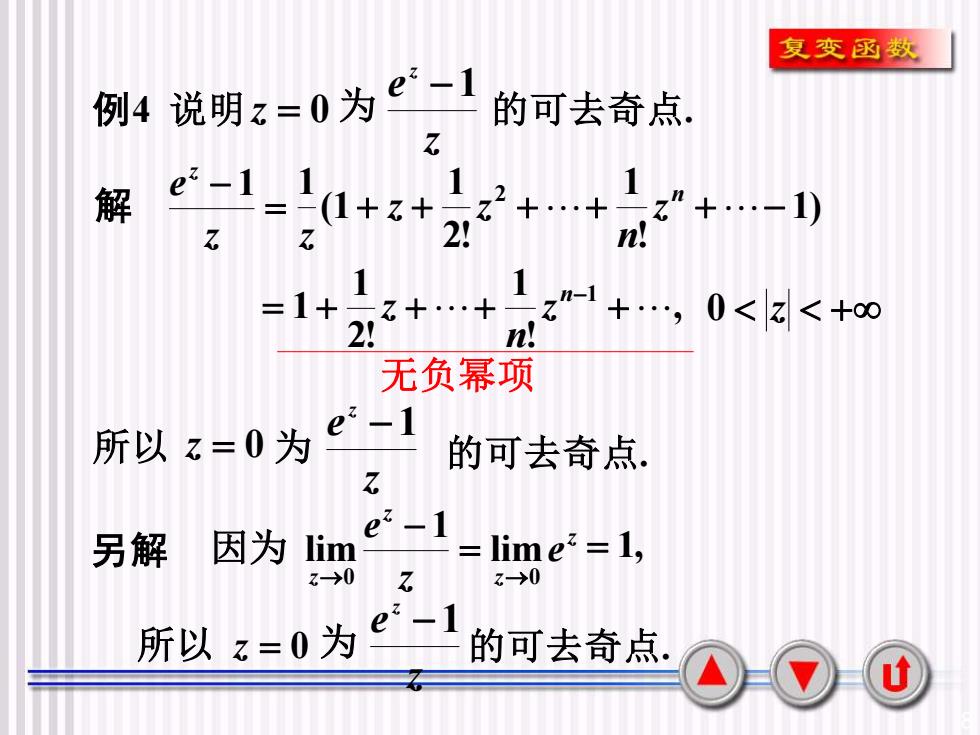
8 例4 说明 z = 0 为 z e z −1 的可去奇点. 解 = − z e z 1 , ! 1 2! 1 1 = + ++ z n−1 + n z 0 z + 所以 z = 0 为 的可去奇点. z e z −1 无负幂项 另解 z z z z e z e 0 0 lim 1 lim → → = − 因为 所以 z = 0 为 的可去奇点. z e z −1 1) ! 1 2! 1 (1 1 2 + + ++ +− n z n z z z = 1

复变函数2.极点1)定义如果洛朗级数中只有有限多个z一z的负幂项,其中关于(z一zo)-的最高幂为(z一zo)-m即f(z)= C-m(z- zo)-m + -+ C-2(z- zo)-2 + C_i(z - zo)-1(m ≥ 1, c-m ± 0)+ Co + c,(z- zo) +.:1或写成f(z) =mg(z)(Z-Z0)那末孤立奇点Zo称为函数f(z)的m级极点u
9 2. 极点 1 1 0 2 0 2 0 ( ) ( ) ( ) ( ) − − − − − − f z = c z − z + + c z − z + c z − z m m ( 1, 0) −m + + ( − ) + m c 0 1 0 c c z z ( ) , ( ) 1 ( ) 0 g z z z f z m − = 1 0 ( ) − z − z ( ) , 0 m z z − 其中关于 的最高幂为 − 即 那末孤立奇点 z0 称为函数 f (z) 的 m 级极点. 或写成 1) 定义 0 如果洛朗级数中只有有限多个 z − z 的 负幂项

复变函数说明:(1)g(z) = C-m + C-m+1(z - zo) + C-m+2(z - zo)2 + ..特点:1.在z-Zol<8内是解析函数2. g(zo) ± 0(2)如果 zo 为函数 f(z)的极点,则lim f(z) = 00.Z>Z03z + 2例5 有理分式函数 f(z)== 2(z + 2)=0是二级极点,=-2 是一级极点U
10 说明: g(z) = c−m + c−m+1 (z − z0 ) + c−m+2 (z − z0 ) 2 + 1. 在z − z0 内是解析函数 2. g(z0 ) 0 特点: (1) (2) 如果 z0 为函数 f (z) 的极点 , 则 lim ( ) . 0 = → f z z z 例5 有理分式函数 , ( 2) 3 2 ( ) 2 + + = z z z f z z = 0是二级极点, z = −2 是一级极点