
第七节矩阵的秩 定义19在m×n矩阵A中任取r行、r列 (r<min{m,n}),位于这些行与列交叉处的 元素所构成的r阶行列式,称为矩阵A的r 阶子式。 定义20当A0时,A中非零最高阶子 式的阶数,称为矩阵A的秩,记为R(A) (或秩A);当A=0时,规定R(A)=0
第七节 矩阵的秩 定义19 在m×n矩阵A中任取r行、r列 (r≤min{m,n}),位于这些行与列交叉处的 元素所构成的r阶行列式,称为矩阵A的r 阶子式。 定义20 当A≠0时,A中非零最高阶子 式的阶数,称为矩阵A的秩,记为R(A) (或秩A);当A=0时,规定R(A)=0

定理5矩阵的初等变换不改变矩阵的秩 设 A=(aj)mxn R(A)=r a11 a12 a+kaj an kaj A itkr, an aj2 回
A a R A r 设 = ( i j) mn ( ) = + + + ⎯⎯⎯→ + m m m n j j j n i j i j i n j n n r kr a a a a a a a k a a k a a k a a a a A i j 1 2 1 2 1 1 2 2 1 1 1 2 1 定理5 矩阵的初等变换不改变矩阵的秩

如果r=0,则A为零矩阵,B也为零矩 阵,R(B)=0.定理得证 如果r>0,由R(A)=r知,A中所有的 ”+阶子式全为0。在B中任取一个 ”+阶子式D,讨论如下: (I)如果D中不含有第i行,则D是A的 r+1阶子式,于是D=0。 上页
阵, 定理得证 如果 则 为零矩阵, 也为零矩 ( ) 0. r 0, = = R B A B 阶子式 讨论如下: 阶子式全为 。在 中任取一个 如果 由 知, 中所有的 1 , 1 0 r 0, R(A) r r D r B A + + = 阶子式,于是 。 如果 中不含有第 行,则 是 的 1 D 0 (1) i D r + = D A

(2)如果D中同时含有i,j两行,则D 与A中对应位置的r+阶子式相等, 故仍有D=0。 (3)如果D中包含第行,不包含第行, D-an+kan dn+kap.am+kam 上页 返回
故仍有 。 与 中对应位置的 阶子式相等, 如果 中同时含有 , 两行,则 D 0 1 (2) i j D = A r + D (3)如果D中包含第i行,不包含第j行, i j i j i n j n D = a 1 + k a 1 a 2 + k a 2 a + k a
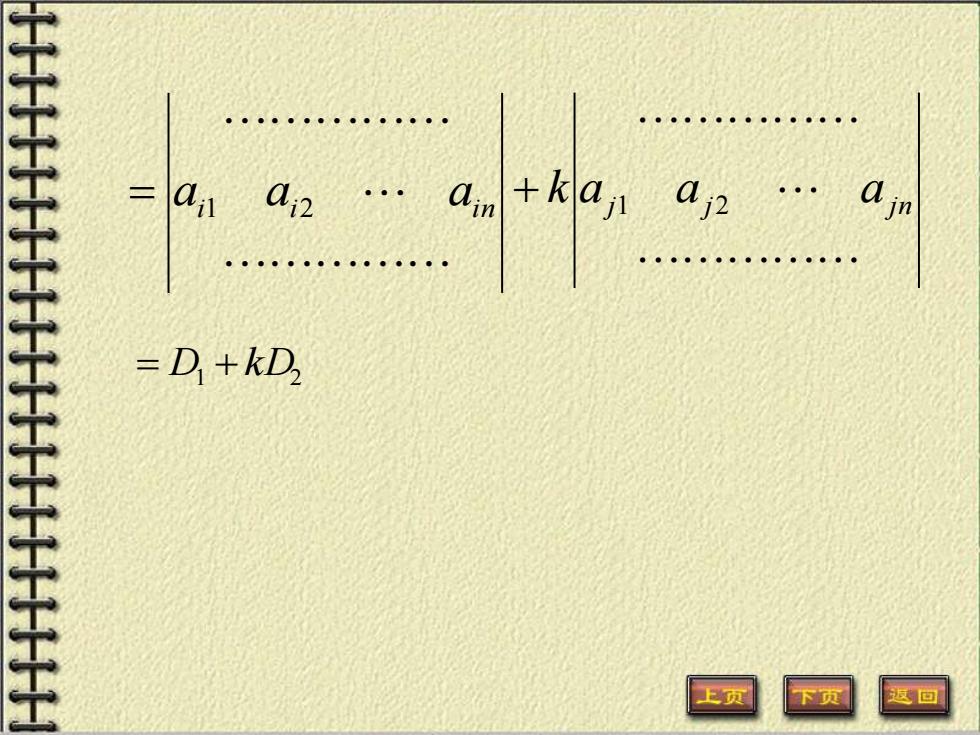
=D+kD 上页 下页 回
= ai1 ai2 ai n aj aj aj n k + 1 2 1 2 = D + kD