
第三节行列式的性质 口用于化简和计算行列式 」用于理论推导和证明
第三节 行列式的性质 ◼ 用于化简和计算行列式 ◼ 用于理论推导和证明
设 D 02 02 则称 d22 0n2 为D的转置行列式,记为D
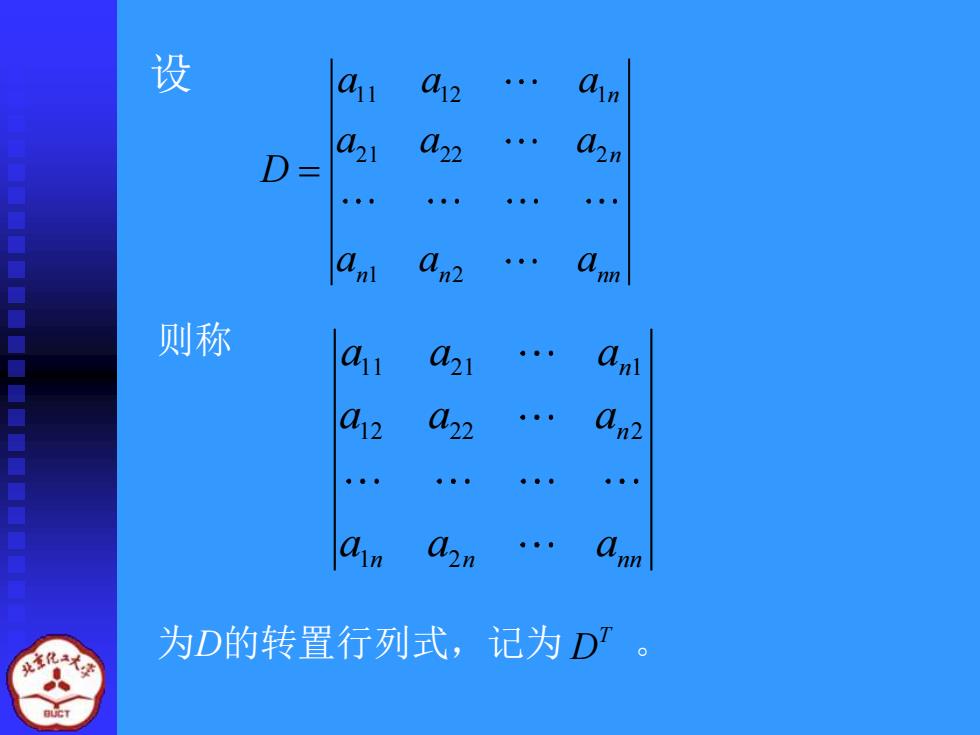
设 11 12 1 21 22 2 1 2 n n n n nn a a a a a a D a a a = 则称 11 21 1 12 22 2 1 2 n n n n nn a a a a a a a a a 为D的转置行列式,记为 D T

性质1行列式等于它的转置行列式,即D=D 记b=ai,1≤1,j≤n 则 b21 。。d 。。 n2 b = ∑(lw5'a4e…a. hj2In =D
性质1 行列式等于它的转置行列式,即 T D D= 证明 记 则 11 12 1 21 22 2 1 2 n T n n n nn b b b b b b D b b b = , 1 , , ij ji b a i j n = 1 2 1 2 1 2 1 2 1 2 1 2 ( ) 1 2 ( ) 1 2 ( 1) ( 1) n n n n n n j j j j j j n j j j j j j j j nj j j j a a a a a a D = − = − =

由性质1,行与列的地位是对称的,对行成立 的性质对列也成立,反之亦然。以下的叙述与 证明只对行给出。 性质2两行(列)互换, 行列式值改变符号, 即 a 02 00 a n
由性质1,行与列的地位是对称的,对行成立 的性质对列也成立,反之亦然。以下的叙述与 证明只对行给出。 性质2 两行(列)互换,行列式值改变符号, 即 1 2 1 2 1 2 1 2 j j jn i i in i i in j j jn a a a a a a a a a a a a = −

证明记等式右边的行列式为D,它的第, 行互换,得到等式左边的行列式,记为D。 注意D的第i,j元素行指标依次为ji,可得 D=∑(s5'a。…a6…a…a ……… =-∑(4aa影a%…a =-D
证明 记等式右边的行列式为D,它的第 i, j 行互换,得到等式左边的行列式,记为D1。 注意D1的第 i, j 元素行指标依次为 j, i, 可得 1 1 ( ) 1 1 ( ) 1 ( 1) ( 1) i j i j n i j j i j i n j i t t t jt it nt t t t t t it jt nt t t D a a a a a a a a D = − = − − = −