北京化工大学：《线性代数》课程教学资源（PPT课件）第三章 线性方程组 第四节 矩阵秩与向量组秩的关系

第四节矩阵秩与向量组秩的关系 ☒无法显示该图片 1 2 设A= 02N 02 是mxn的矩阵 m2 mn

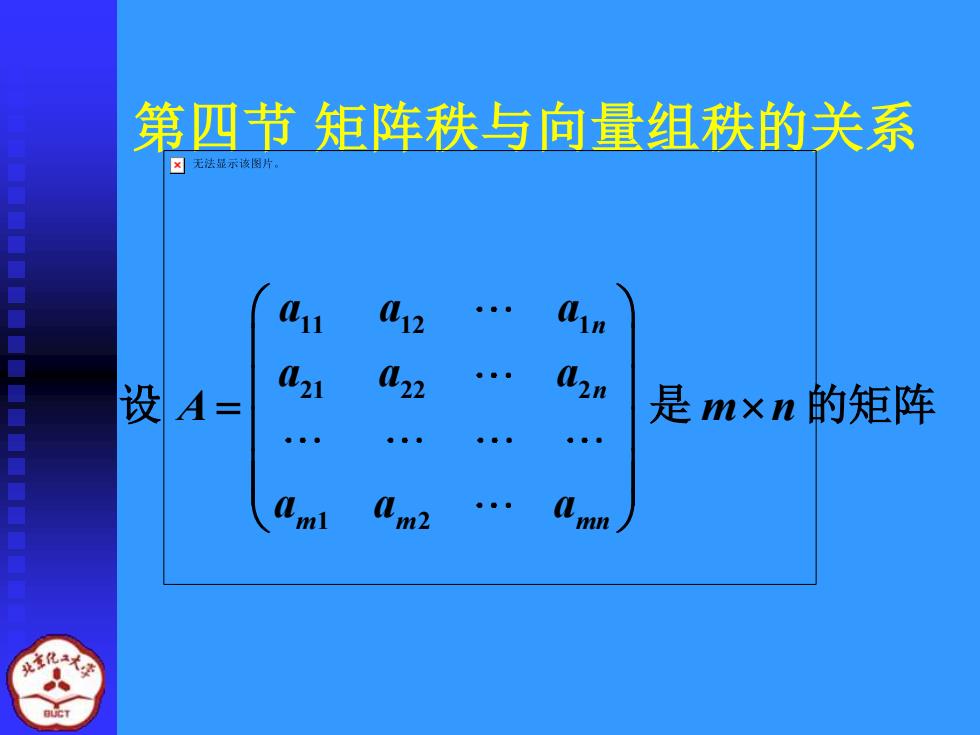
第四节 矩阵秩与向量组秩的关系 11 12 1 21 22 2 1 2 n n m m mn a a a a a a A m n a a a       =        设 是 的矩阵

按行分块得到 A= B. 其中p=(a1,42,…un) 是A的第行构成的向量 (年1,2，…m

按行分块得到 1 2 m A          =       ( ) ( ) 1 2 , , i i in a a a A i 其中 i = 是 的第 行构成的向量 i= 1,2, m

将该矩阵按列分块得到 A=(aag2… j 其中0，= 是A的第例构成的 向量（手1,2，…n）

将该矩阵按列分块得到 A= (   1 2 n ) 1 2 j j j mj a a a        =         其中 ( ) A n 是 的第j列构成的 向量 j= 1,2

{f,…pnm} 称为A的行向量组 {ap…on} 称为A的列向量组 定义9矩阵A的行向量组的秩成为A 的行秩，A的列向量组的秩称为A的 列秩。 矩阵A的秩与其行秩和列秩有 什么关系呢？

  称为A的行向量组  1  , m n     1 ， 称为A的列向量组 定义9 矩阵A的行向量组的秩成为A 的行秩，A的列向量组的秩称为A的 列秩。 矩阵A的秩与其行秩和列秩有 什么关系呢？

先看一个例子 0 B 此矩阵为具有4个非零行的 B-型矩阵

先看一个例子 1 1 2 2 3 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 a b a b B b       =           此矩阵为具有4个非零行的 B-型矩阵