
解向量可写成 故 f=2a1-3a 所以,向量B 可由向量组C1,02 线性表出
解向量可写成 x x 骣ç ÷ 骣ç ÷ ç ÷= ç ÷ ç桫 ÷÷ ç桫- ÷÷ 故 β = α - α 所以,向量 可由向量组 线性表出. β , α α

例5减肥配方问题 设三种食物每100克中蛋白质、碳水化合 物和脂肪的含量如下表3.1.1,表中还给 出了20世纪80年代美国流行的简洁营养配 方。如果用这三种食物作为每天的主要食 物,那么它们的用量应各取多少,才能全 面准确地实现这个营养要求?
例 5 减肥配方问题 设三种食物每100克中蛋白质、碳水化合 物和脂肪的含量如下表3.1.1,表中还给 出了20世纪80年代美国流行的简洁营养配 方. 如果用这三种食物作为每天的主要食 物,那么它们的用量应各取多少,才能全 面准确地实现这个营养要求?
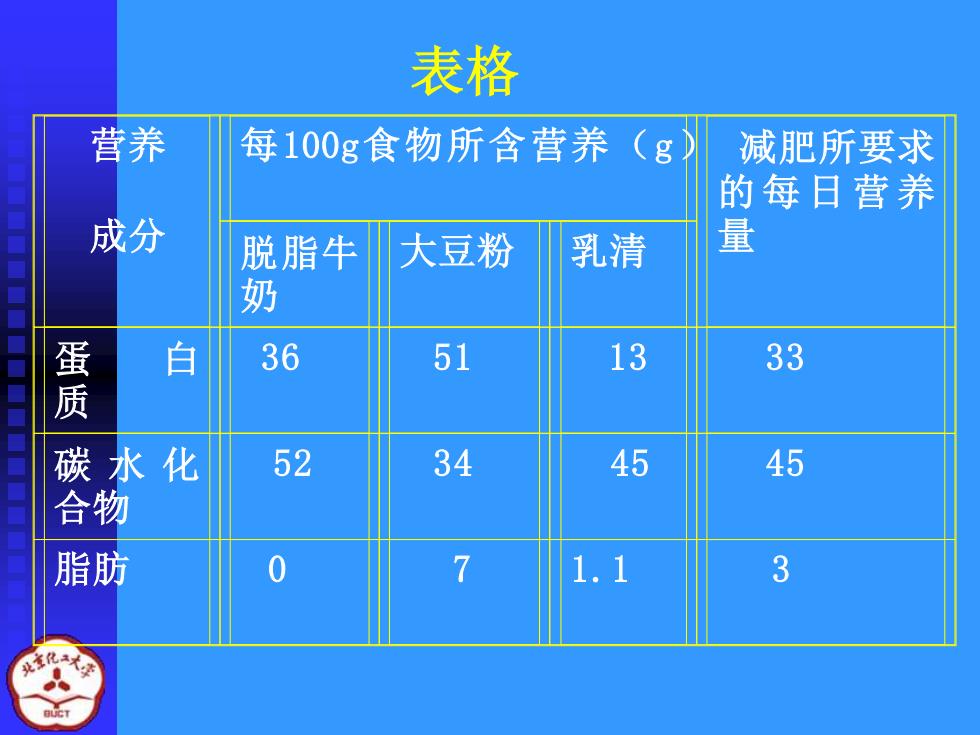
表格 营养 每100g食物所含营养(g 减肥所要求 的每日营养 成分 脱脂牛 大豆粉 乳清 量 奶 蛋质 白 36 51 13 33 碳合 水化 52 34 45 45 0 7 1.1 3
营养 成分 每100g食物所含营养(g) 减肥所要求 的每日营养 脱脂牛 量 奶 大豆粉 乳清 蛋 白 质 36 51 13 33 碳水化 合物 52 34 45 45 脂肪 0 7 1.1 3 表格

设脱脂牛奶、大豆粉和乳清用量 分别为x1,x2,x3个单位(100g) 三种食物所含营养的列向量分别为 a1=(36,52,0)7, a2=(51,34,7)7, a3=13,74,1.1) 每日所需营养量的列向量为 B=(33,45,3)1
设脱脂牛奶、大豆粉和乳清用量 分别为 x x x , , 个单位(100g) ( , , ) , ( , , ) , ( , , . ) T T T α α α = = = ( , , )T β = 三种食物所含营养的列向量分别为 每日所需营养量的列向量为

由题意 三种食物每日所需量的多少恰好为向量 B由向量组 a1,02和a3 线性表示的系数,所以, x%1+x2C2十x3a3=B 即 34
由题意 三种食物每日所需量的多少恰好为向量 由向量组 α , α 和 线性表示的系数,所以, β α x x x α α α β + + = . x x x 骣 骣 骣 珑 鼢鼢 ? ? 珑 鼢 ? ? 珑 鼢 ? ? 珑 鼢 = ? ? 珑 ? 珑 鼢 ? ? 鼢 ? ? 琪珑桫 ÷鼢珑桫 桫? ? 即 , α α β α , α α β α , α α