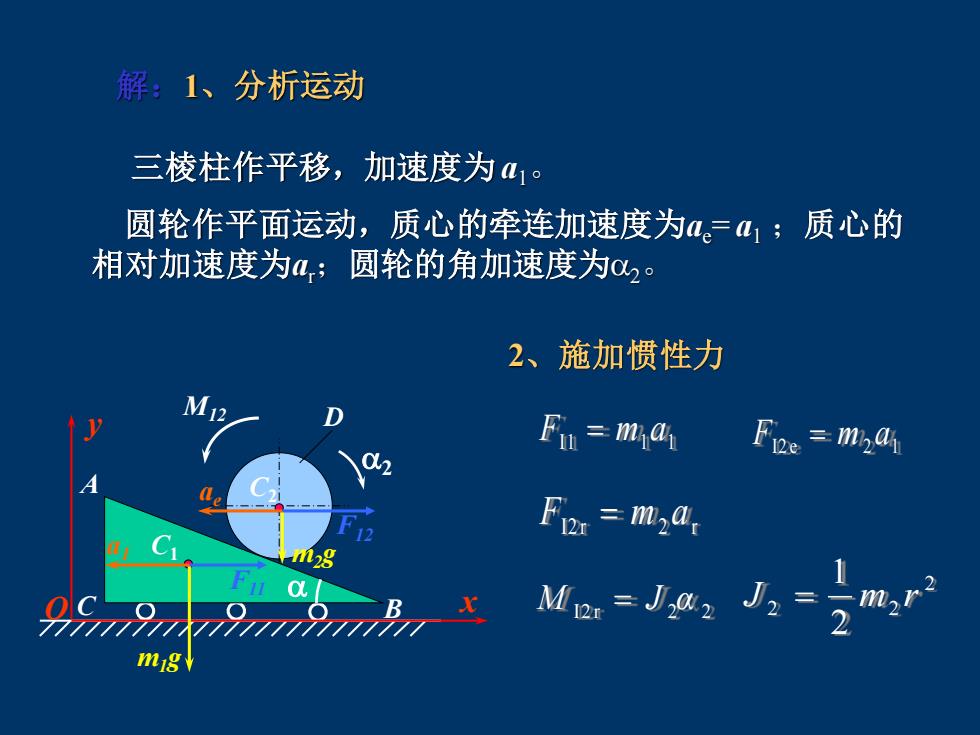
解:1、分析运动 三棱柱作平移,加速度为41s 圆轮作平面运动,质心的牵连加速度为a.=41;质心的 相对加速度为a;圆轮的角加速度为02。 2、施加惯性力 Fi =mid Fios =mad F=m,4, n28 Mes=m mig
解:1、分析运动 三棱柱作平移,加速度为a1。 圆轮作平面运动,质心的牵连加速度为ae= a1 ;质心的 相对加速度为ar;圆轮的角加速度为2。 2、施加惯性力 I1 1 1 F = m a I2 e 2 1 F = m a I2 r 2 r F = m a I2 r 2 α 2 M = J 2 2 2 2 1 x J = m r y C2 D C1 A C B O m1g m2g a1 ae F12 F11 M12 2
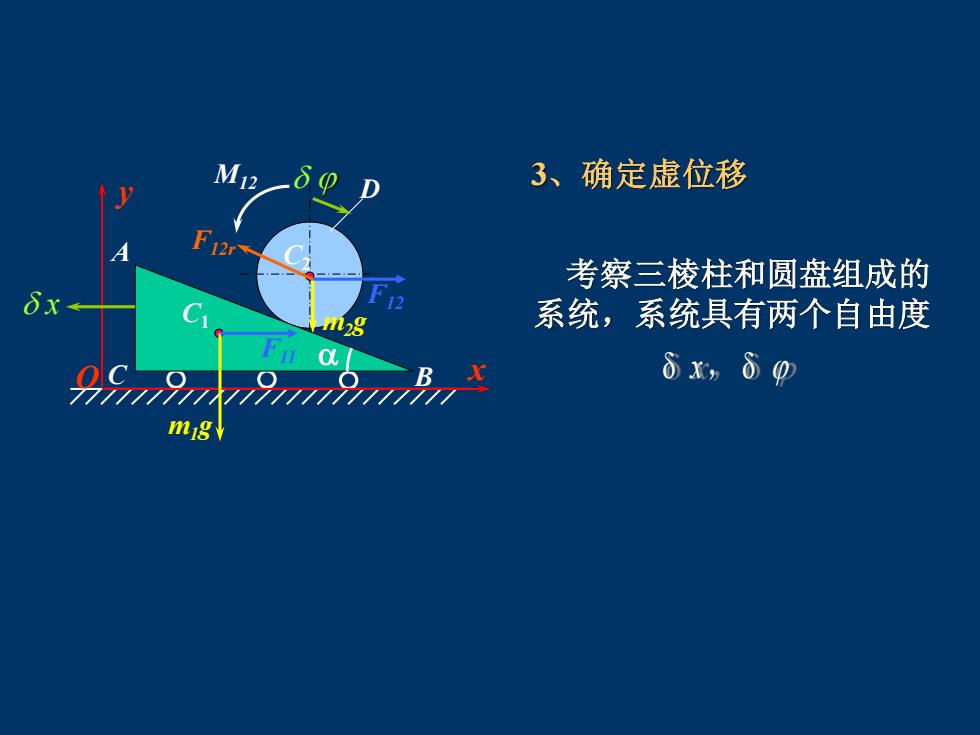
3、确定虚位移 12r 考察三棱柱和圆盘组成的 m28 系统,系统具有两个自由度 dx,60
3、确定虚位移 考察三棱柱和圆盘组成的 系统,系统具有两个自由度 x δ x, δ y C2 D C1 A C B O m1g m2g F12r F12 F11 M12 x

4、应用达朗贝尔一拉格朗日方程 令0x=0, 60≠0 magsimaRo FizecosaR p-FizrRo oJaR =0 3 sin a+-(a cosa- 8 4)=0 令6x≠0,60=0 -(in+fi2e)心+fc0sòX=0 (m1±m2a4 a= mcosa 求解联立方程,得: magsin2 a 4≡ n28 3(m1+m2)厂2m2c0sa a- 2gsin a(m+m2) 3(m1+m2-2m2c0s2a
令 δx = 0, δ 0 sin δ co s δ δ δ 0 2 I 2 e I 2 r 2 2 m g R + F R − F R - J R = ) 0 2 3 ( cos 1 sin + a1 − ar = g 4、应用达朗贝尔-拉格朗日方程 令 δ x 0, δ = 0 ( )δ co s δ 0 I1 I 2 e I 2 r − F + F x + F x = cos ( ) 1 2 1 r m m m a a + = 求解联立方程,得: 2 1 2 2 1 2 r 2 1 2 2 2 1 3( ) 2 cos 2 sin ( ) 3( ) 2 cos sin2 m m m g m m a m m m m g a - - + + = + = x y C2 D C1 A C B O m1g m2g F12r F12 F11 M12 x

4基本拉格朗日方程 由于约束条件,个矢径并不独立.现在引入独立的广义 坐标q。把矢径用广义坐标表示出 元=7(g1,92,9,) 以,.S 对时间求导 因为位矢只是广义坐标和时间的函数,它对广义坐标的 偏导数也是广义坐标和时间的函数,因此速度就是广义 坐标、广义速度以及时间的函数,但是位矢对时间和 广义坐标的偏导数并不是广义速度的函数
由于约束条件, n个矢径并不独立. 现在引入独立的广义 坐标q把矢径用广义坐标表示出 ( , , , ; ) 1 2 r r q q q t i i s = 对时间求导 d d d d 1 t q q r t r t r s i i i = + = 因为位矢只是广义坐标和时间的函数, 它对广义坐标的 偏导数也是广义坐标和时间的函数, 因此速度就是广义 坐标、广义速度以及时间的函数, 但是位矢对时间和 广义坐标的偏导数并不是广义速度的函数. 4 基本拉格朗日方程

因为广义速度也是互相独立的,所以 (5.24) 再来看位矢对广义坐标的偏导数的时间变化率 qqa 98+ 5.25 即位矢对广义坐标的偏导数和对时间的偏导数可以对易
因为广义速度也是互相独立的, 所以 (5.24) 1 1 q r q q q r q q r t r q q r i s i s i i i = = + = = = 再来看位矢对广义坐标的偏导数的时间变化率 (5.25) d d d d 1 2 1 2 = + = + = = = t r t q r q q r t q q r q q q r q r t i i s i i s i i 即位矢对广义坐标的偏导数和对时间的偏导数可以对易