
下面六个例题, 需要数学软件, 请分六组完成
下面六个例题, 需要数学软件, 请分六组完成

例1、单摆是由一质量为的质点用长为 L的弦或者轻杆悬挂在点O构成的.假定弦 不能伸长,且质量可以忽略.研究单摆的运 动规律, 解:分析受力,得到运动方程为 径向:mg cos0-F=m(-L02) (1) mg 横向:-mg sin0=mL0 (2) 改写方程(2) +sin0=0 (3) 对于小角度,sin00,方程简化为 6+80=0 通解为0=Acos(ot+p,) 考虑初始条件0(t=0)=0,0(t=0)=0
例1、单摆是由一质量为m的质点用长为 L的弦或者轻杆悬挂在点O构成的. 假定弦 不能伸长,且质量可以忽略.研究单摆的运 动规律. O L FT mg 解: 分析受力, 得到运动方程为 径向: 横向: cos ( ) 2 mg − FT = m −L (1) mg mL − sin = (2) 改写方程(2) 对于小角度, sin~, 方程简化为 + = 0 L g 通解为 ( ) 0 = Acos t + 考虑初始条件 ( 0) , ( 0) 0 t = =0 t = = + sin = 0 L g (3)

得到解 0=日cos(@,),o-g 对于一般情况,方程(3)可积分一次得到 dodθ =sin0->0d0-sin Od0 do di L 6=2(os0-eos8】 完整的解需要特殊函数,我们作图可以看出:角度越 大,频率越低,不是固定频率的形式: 其实只要我们简单考虑(3) 0 =0 就可以看出频率随角度的变化
( ) 2 0 0 0 cos , g t L 得到解 = = 对于一般情况, 方程(3)可积分一次得到 ( ) 2 0 sin sin 2 cos cos d d g g d d d dt L L g L = = − → = − = − 完整的解需要特殊函数,我们作图可以看出:角度越 大, 频率越低,不是固定频率的形式. 其实只要我们简单考虑(3) 0 sin = + L g 就可以看出频率随角度的变化
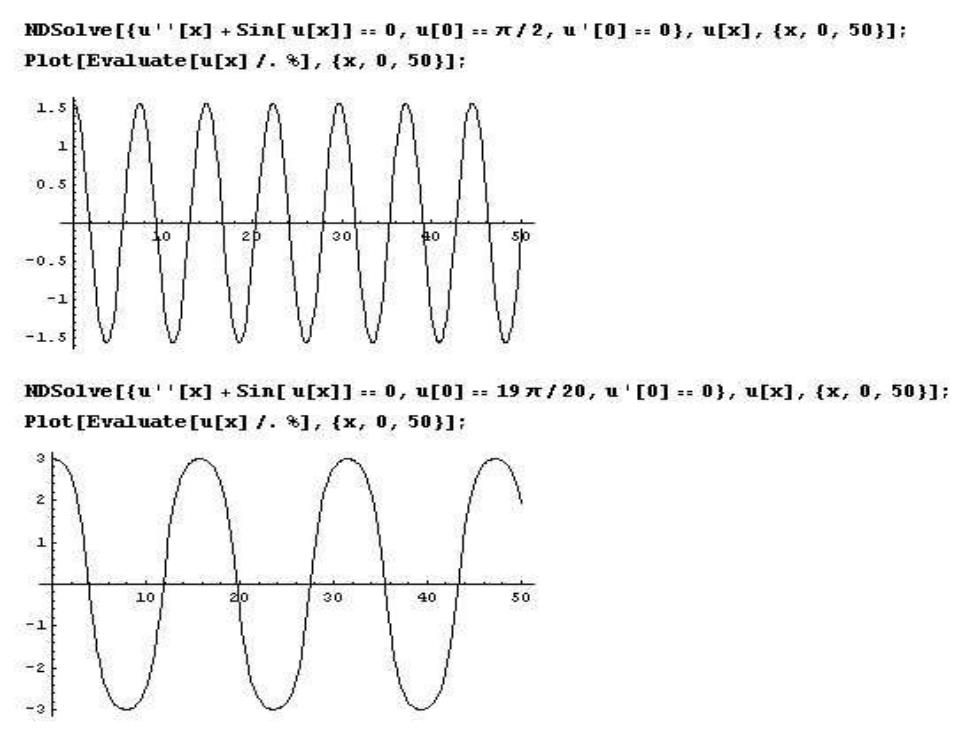
DSo1ve[{u''[x]+Sin[u[x]]=s0,u[0]=π/2,u'[0]=:03,u[x],{x,0,50}]: P1ot[Eva1uate[u[x]/.%],{x,0,50}]: DSo1ve[{u''[x]+sin[u[x]]-=0,u[0]=19π/20,u'[0]=0,u[x],{x,0,50)]: P1ot[Evaluate[u[x]/.],{x,0,503]:

例2、单摆是由一质量为m的质点用长为 的轻杆悬挂在某点构成的.假定弦不能 伸长,且质量可以忽略.(1)以角度为参数 做势能曲线,说明图上哪个范围是小球 能够达到的;(2)对于H=E/mgl=0.1,1,2, 3.5,试做角速度与角位移曲线,并讨论它 们各自对应的单摆运动情况;3)求小振 mg 幅时的周期. 解:(1)单摆的重力势能为 V(0)=mgl(1-cose) 曲线如图所示,它在0=0处有极小值,即这里是稳定平衡点 表示总能量E的水平线与势能曲线之间相差的高度代表 动能E,因为动能恒正,所以运动只能在势能曲线低于水 平线的范围内才能实现,则虚线的位置标示着振幅!
例2、单摆是由一质量为m的质点用长为 l的轻杆悬挂在某点构成的. 假定弦不能 伸长,且质量可以忽略.(1)以角度为参数 做势能曲线,说明图上哪个范围是小球 能够达到的; (2)对于H = E/mgl =0.1, 1, 2, 3.5, 试做角速度与角位移曲线, 并讨论它 们各自对应的单摆运动情况; (3) 求小振 幅时的周期. l mg 解: (1)单摆的重力势能为 V() = mgl(1− cos ) 曲线如图所示,它在 = 0处有极小值,即这里是稳定平衡点. 表示总能量E的水平线与势能曲线之间相差的高度代表 动能Ek . 因为动能恒正, 所以运动只能在势能曲线低于水 平线的范围内才能实现, 则虚线的位置标示着振幅