图5-11应用零阶保持器恢复信号 零阶保持器的频率特性为 @T G,0o)=1-e"Tg .e2-e sin OT T =T2 -1 2 -e jo 2j ⊙T 2 2 (5-22)
图 5-11 应用零阶保持器恢复信号 零阶保持器的频率特性为 2 2 2 2 2 2 sin 2 2 1 ( ) T j T j T j T j j T h e T T T j e e e T T j e G j − − − − = − = − = (5-22)
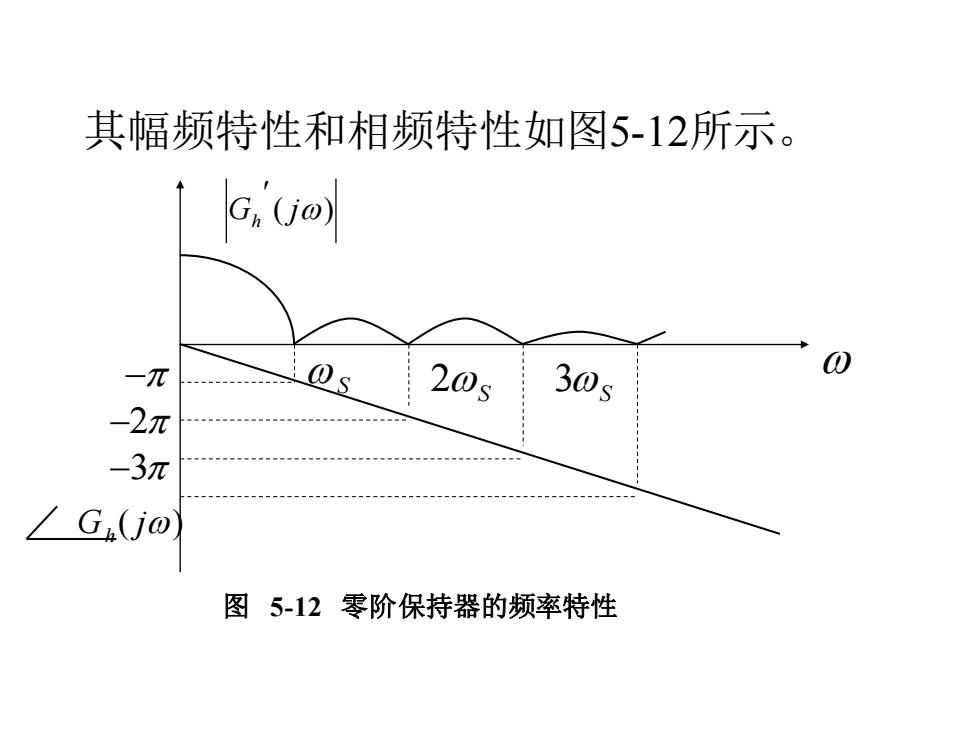
其幅频特性和相频特性如图5-12所示。 G,o) -π 20s 30s 0 -2π -3π 人G(j0 图5-12零阶保持器的频率特性
其幅频特性和相频特性如图5-12所示。 G ( j) h S 2S 3S − −2 −3 G ( j) h 图 5-12 零阶保持器的频率特性

5.4Z变换理论 5.4.1z变换 5.4.2z变换的性质 5.4.3z反变换
5. 4 Z变换理论 5.4.1 z 变换 5.4.2 z 变换的性质 5.4.3 z 反变换

5.4.1Z变换 由式(5-5)可知,x*()的拉氏变换为 x(s)=∑x(kTe (5-28) k=0 若令 e (5-29) 则$域分析的问题变成Z域的分析问题。 x(z)=∑x(kT)z (5-30) k=0
5.4.1 Z变换 由式(5-5)可知,x*(t)的拉氏变换为 (5-28) 若令 (5-29) 则S域分析的问题变成Z域的分析问题。 0 ( ) ( ) k k x z x kT z − = = (5-30) * 0 ( ) ( ) kTs k x s x kT e − = = Ts e z =

x(2)称为x*(①)的z变换,记为Z[X*() [X*(t)]=x(=)=>x(kT)=k (6-31) 在Z变换中,(2)为采样脉冲序列的Z变换, 即只考虑采样时刻的信号值。由于在采样时 刻,x(z)的值就是xkT),所以从这个意义上说 ,x(z)既是x*(t)的Z变换,也可以写为x(t)的Z 变换,即 Z[x*(]=[x(]=x(e)=∑x(k7)2 k=0 (5-32)
x(z)称为x*(t)的z 变换,记为 Z X t *( ) 0 *( ) ( ) ( ) k k Z X t x z x kT z − = = = (5-31) 在Z变换中, x(z) 为采样脉冲序列的Z变换, 即只考虑采样时刻的信号值。由于在采样时 刻,x(z)的值就是x(kT),所以从这个意义上说 , x(z) 既是x*(t)的Z变换,也可以写为x(t)的Z 变换,即 (5-32) 0 *( ) [ ( )] ( ) ( ) k k Z x t z x t x z x kT z − = = = =