
第二章 控制系统数学模型
控制系统数学模型 第二章

提要 1.描述系统各变量之间关系的数学表达式,叫做 系统的数学模型。实际存在的系统的动态性 能都可以通过数学模型来描述(例如微分方 程、传递函数等)。 2.建立合理的控制系统数学模型是控制系统分析 中最重要的内容,与系统性能密切相关。本 章将对系统和元件的数学模型建立、传递函 数概念、结构图和信号流图的建立及简化等 内容加以论述
提要 1.描述系统各变量之间关系的数学表达式,叫做 系统的数学模型。实际存在的系统的动态性 能都可以通过数学模型来描述(例如微分方 程、传递函数等)。 2.建立合理的控制系统数学模型是控制系统分析 中最重要的内容,与系统性能密切相关。本 章将对系统和元件的数学模型建立、传递函 数概念、结构图和信号流图的建立及简化等 内容加以论述

数学模型分为动态模型与静态模型。 a.控制系统的动态模型是指描述变量各阶导数之间关系的微分 方程。即线性定常微分方程,可由此分析系统的动态特性。 b.控制系统的静态模型是指在静态条件下(即变量的各阶导数 为零),描述变量之间关系的代数方程。 建立系统数学模型时,必须: ()全面了解系统特性,确定研究目的以及准确性要求,决定 能否忽略一些次要因素而简化系统的数学模型。 (2)根据所应用的系统分析方法,建立相应形式的数学模型。 建立系统的数学模型主要有两条途径: 1.分析法。 2.实验法。即根据对系统的观察,通过测量所得到的输入、输 出数据,推断出系统的数学模型
数学模型分为动态模型与静态模型。 a.控制系统的动态模型是指描述变量各阶导数之间关系的微分 方程。即线性定常微分方程,可由此分析系统的动态特性。 b.控制系统的静态模型是指在静态条件下(即变量的各阶导数 为零),描述变量之间关系的代数方程。 建立系统数学模型时,必须: (1) 全面了解系统特性,确定研究目的以及准确性要求,决定 能否忽略一些次要因素而简化系统的数学模型。 (2) 根据所应用的系统分析方法,建立相应形式的数学模型。 建立系统的数学模型主要有两条途径: 1.分析法。 2.实验法。即根据对系统的观察,通过测量所得到的输入、输 出数据,推断出系统的数学模型

第一节控制系统的时域数学模型 控制系统的运动状态和动态性能可由微分方程 式描述,微分方程式是系统的一种数学模型。建立 系统微分方程的一般步骤如下: (1)适当简化,忽略一些次要因素。 (2)根据元件的物理或化学定律,列出相应的微分 方程式。 (③)消去中间变量,推出元件的输入量和输出变量 之间关系的微分方程。 (4)求出其它元件的方程。 (⑤)从所有元件的方程式中消去中间变量,最后得 到系统的输入输出微分方程
第一节 控制系统的时域数学模型 控制系统的运动状态和动态性能可由微分方程 式描述,微分方程式是系统的一种数学模型。建立 系统微分方程的一般步骤如下: (1) 适当简化,忽略一些次要因素。 (2) 根据元件的物理或化学定律,列出相应的微分 方程式。 (3) 消去中间变量,推出元件的输入量和输出变量 之间关系的微分方程。 (4) 求出其它元件的方程。 (5) 从所有元件的方程式中消去中间变量,最后得 到系统的输入输出微分方程
(一)RL-C电路 图2-1所示R-L-C电路中,R、L、,C均为常值,U(⑤为输入电压, u()为输出电压,输出端开路。求出u)与u①的微汾方程。 十0 () ud(t) 图2-1R-L-C无源电路 (1)根据克希霍夫定律可写出原始方程式: i+i0ot+0=e0 (2.1)
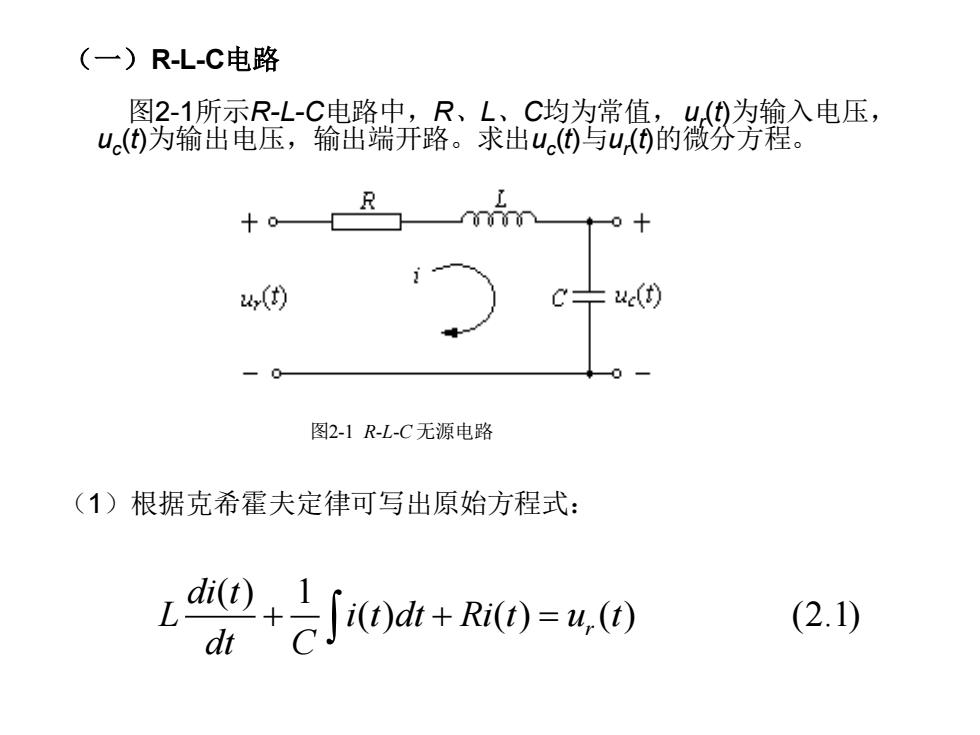
(一)R-L-C电路 图2-1所示R-L-C电路中,R、L、C均为常值,ur (t)为输入电压, uc (t)为输出电压,输出端开路。求出uc (t)与ur (t)的微分方程。 (1)根据克希霍夫定律可写出原始方程式: 图2-1 R-L-C 无源电路 ( ) 1 ( ) ( ) ( ) (2.1) r di t L i t dt Ri t u t dt C + + =