南阳师范学院：《高等数学》课程教学课件（同济第六版）第七章 微分方程的基本概念 7.4 一阶线性微分方程

第四节一阶线性微分方程

第四节 一阶线性微分方程

一、有关的概念 方程会+y=Qx)叫做一阶线性微分方程其中P,Q)为已知函数 已知函数 只含未知函数 的一阶导数且 +Py=Q 系数为1 dx 已知函数 未知函数是一 次的 如果Q()=0,则方程称为齐次线性方程，否则方程称为非齐次线性方程 方程密+代y-0叫做对应于非齐次线性方程密代-Q的齐次线性方程 dx

方程 P(x)y Q(x) dx dy   叫做一阶线性微分方程其中P x Q x ( ), ( ) 为已知函数. 一、有关的概念 P(x)y Q(x) dx dy   如果 Q x( ) 0   则方程称为齐次线性方程 否则方程称为非齐次线性方程 方程 P(x)y0 dx dy 叫做对应于非齐次线性方程 P(x)y Q(x) dx dy   的齐次线性方程 已知函数 已知函数 只含未知函数 的一阶导数且 系数为1 未知函数是一 次的

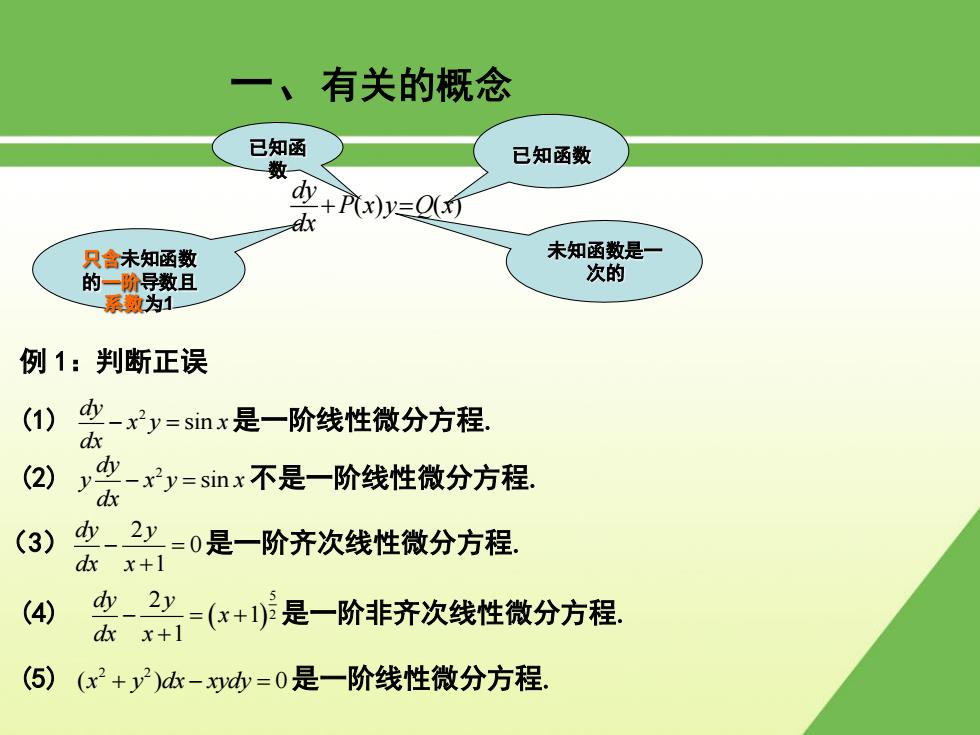
一、有关的概念 已知函 已知函数 数 +Pxy=O dx 只含未知函数 未知函数是一 的一阶导数且 次的 系数为1 例1：判断正误 (1) -xy=sinx是一阶线性微分方程 d (2) -x2y=sinx不是一阶线性微分方程， dx (3) 少-2少=0是一阶齐次线性微分方程。 dx x+1 (4) 少-2少=x+1)是一阶非齐次线性微分方程. dx x+1 (5) (x2+y2)dk-3d=0是一阶线性微分方程

一、有关的概念 P(x)y Q(x) dx dy   例 1：判断正误 (1) 2 sin dy x y x dx   是一阶线性微分方程 未知函数是一 次的 已知函数 只含未知函数 的一阶导数且 系数为1 已知函 数 (2) 2 sin dy y x y x dx   不是一阶线性微分方程 （3） 2 0 1 dy y dx x    是一阶齐次线性微分方程 (4)   5 2 2 1 1 dy y x dx x     是一阶非齐次线性微分方程 (5) 2 2 ( ) 0 x y dx xydy    是一阶线性微分方程

二、一阶齐次线性方程的解法 注记1：齐次线性方程会+咖=0是可分离变量的微分方程 定理1：一阶齐次线性方程票+-0的通解是 y=CeJ体(C=士eS)(积分中不再加任意常数). 注记2：解一阶齐次线性方程的步骤 第一步：分离变量：少=-Px, 第二步：两边积分得nl咋∫P(x)d+C, 第三步：求出y=CeP(C=±e9) 就是齐次线性微分方程的通解（积分中不再加任意常数）

二、一阶齐次线性方程的解法 注记 1：齐次线性方程 P(x)y0 dx dy 是可分离变量的微分方程 注记 2：解一阶齐次线性方程的步骤 第一步：分离变量： P x dx y dy  ( )  第二步：两边积分得 1 ln| y| P(x)dxC   就是齐次线性微分方程的通解（积分中不再加任意常数） 定理 1：一阶齐次线性方程 P(x)y0 dx dy 的通解是 ( ) 1 P(x)dx C y Ce Ce    （积分中不再加任意常数） 第三步： 求出 ( ) 1 P(x)dx C y Ce Ce   

三、一阶非齐次线性方程的解法一一常数变易法 定理2：一阶非齐次线性方程会+代ey-Q的通解为 y=CeJP+e JPxk∫ecxe在. 对应的齐次线性方 非齐次线性方程的特解 程通解

定理 2：一阶非齐次线性方程 P ( x ) y Q ( x ) dx dy   的通解为 y Ce e Q x e dx P x dx P x dx P x dx        ( )  ( ) ( ) ( )  三、一阶非齐次线性方程的解法---常数变易法 对应的齐次线性方 程通解 非齐次线性方程的特解