
定理1矩阵A可逆的充要条件是A≠0,且 A 其中A为矩阵A的伴随矩阵 证明若A可逆,即有A使AA=E. 故AA=|E=1,所以A≠0. 回
定理1 矩阵 可逆的充要条件是 ,且 , −1 1 = A A A A A 0 证明 若 A 可逆, A AA = E. 即有 −1使 −1 1, 1 = = − 故 A A E 所以A 0. 其中A 为矩阵A的伴随矩阵.
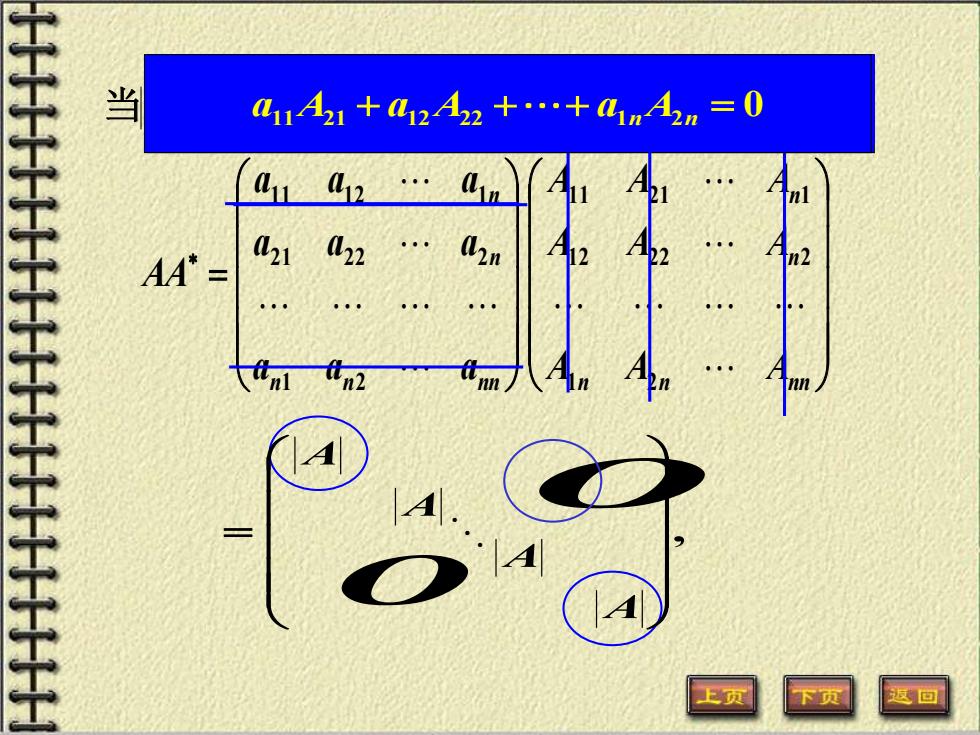
当 411A1+42A2+.+41mA2n=0 AA 021022 上页
当A 0时, = n n nn n n n n nn n n A A A A A A A A A a a a a a a a a a AA 1 2 1 2 2 2 2 1 1 2 1 1 1 2 2 1 2 2 2 1 1 1 2 1 ana1A11nA111++ana212AAn212++++aann1n AAnn1n ==AA , = A A A A O O 11 21 12 22 1 2 0 n n a A a A a A + + + =

A4=AA=AE今AA=A AA A-E, 按逆矩阵的定义得 A-4 证毕 奇异矩阵与非奇异矩阵的定义 当A=0时,A称为奇异矩阵当A≠0时,A称为 非奇异矩阵 由此可得4是可逆阵的充要条件是为非奇异矩阵 上页 回
AA = A A = AE A E, A A A A A = = . 1 A A A − = 按逆矩阵的定义得 证毕 . 0 , , 0 , 非奇异矩阵 当A = 时 A称为奇异矩阵当A 时 A称 为 奇异矩阵与非奇异矩阵的定义 由此可得A是可逆阵的充要条件是A为非奇异矩阵

推论 若AB=E(或BA=E),则B=A1 证明 A·B=E=1,故A≠0, 因而A存在,于是 B=EB=(AAB=A'(AB) -AE-A 证毕 逆矩阵的运算性质 ()若A可逆,则A亦可逆,且(4'=A. 上页
A B = E = 1, 故 A 0, , 因而A −1存在 于是 B = EB (A A)B −1 = A (AB) −1 = 证毕 ( ), . −1 推论 若AB = E 或BA = E 则B = A 证明 (1) , , ( ) . 1 1 1 A A A = A − 若 可逆 则 − 亦可逆 且 − 逆矩阵的运算性质 A E −1 = 1 A − =

(2)若A可逆,数2≠0,则24可逆,且 -八 (3)若A,B为同阶方阵且均可逆,则AB亦可逆,且 (A少B士A 证明 (AB)B-A-)ABB-)4- =AEA=AA=E, (AB)=B-14-1 上页 这回
( ) 2 若A可逆,数 0,则A可逆,且 (3)若A,B为同阶方阵且均可逆,则AB亦可逆,且 ( )( ) ( ) −1 −1 −1 −1 AB B A = A BB A −1 = AEA , 1 = AA = E − ( ) . −1 −1 −1 AB = B A 证明 ( ) = −1 ABB −1 −1 A ( ) . −1 1 −1 A = A