
第一节阶行列式的定义 卫 上页 这回
第一节 n 阶行列式的定义

一、二阶与三阶行列式 用消元法解二元(一次)线性方程组: aux+a2x2=b (0) (1-1) a21x+a22x2=b2 (2) (1)×22: 41122x1+ a12a22X2fb1422, (2)×012: 412421比1十012422X2fb2012, 两式相减消去x2,得 (a1122-41221)x1=b122-b2412; 这回
用消元法解二元(一次)线性方程组: 一、 二阶与三阶行列式 + = + = (2) (1) 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b (1-1) (1)a22: a11a22x1 + a12a22x2 = b1a22, (2)a12: a12a21x1 + a12a22x2 = b2a12, 两式相减消去x2 , 得 (a11a22 – a12a21) x1 = b1a22 – b2a12;

类似地,消去x,得 (a1122-L1221)x2=b2411-b121 当(a11422-41221)≠0时,方程组的解为: y=402-424 七2= 411b2-b1a2i 41L22-4122 122-01202 由方程组()的四个系数确定 为方便记忆,我们引入二阶行列式 D= a11 412 a11a22-a12a21 ) a21 22 其中元素a,的第一个下标i为行指标,第二个下标j为 列指标。即a,位于行列式的第i行第j列
11 22 12 21 1 22 12 2 1 a a a a b a a b x − − = 11 22 12 21 11 2 1 21 2 a a a a a b b a x − − = 当(a11a22 – a12a21) 0时, 方程组的解为: 由方程组(1)的四个系数确定 类似地, 消去x1 , 得 (a11a22 – a12a21) x2 = b2a11 – b1a21; 为方便记忆,我们引入二阶行列式 (1) 1 1 2 2 1 2 2 1 2 1 2 2 1 1 1 2 a a a a a a a a D = = − 其中元素 aij 的第一个下标 i 为行指标,第二个下标 j 为 列指标。即 aij位于行列式的第 i 行第 j 列
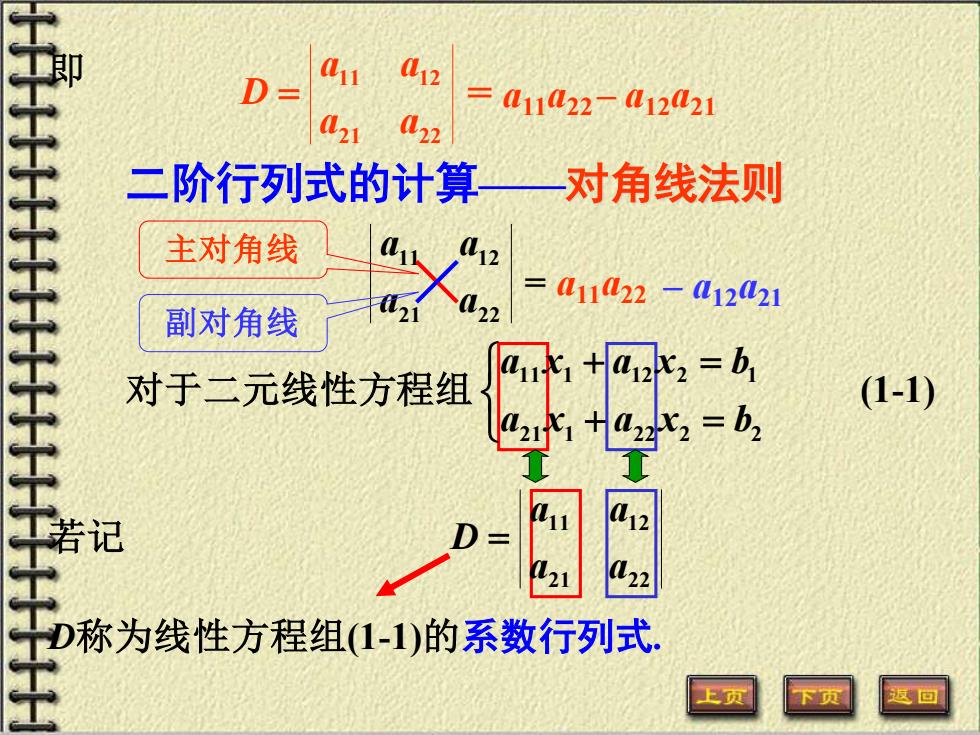
D= 011 12 411022-012021 021 22 二阶行列式的计算— 对角线法则 主对角线 011L22-41221 副对角线 对于二元线性方程组 (1-1) 若记 2 称为线性方程组(1-1)的系数行列式 回
21 22 11 12 a a a a 21 22 11 12 a a a a D = = a11a22 – a12a21 即 主对角线 副对角线 二阶行列式的计算——对角线法则 = a11a22 – a12a21 对于二元线性方程组 D称为线性方程组(1-1)的系数行列式. + = + = 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b 21 22 11 12 a a a a 若记 D = (1-1)

4x+0x au+anx2 021X1+022X2 a2X1+022 b D. 2 b, D2 22 2 b, X1= b122-412b2 七2= 41b2-b1421 (3) 41142-412021 01122-012021 b 12 11 b D1 b, 22 : 21 B, D du 12 X2= D 41 12 王王 21 L22 021 L22 注意:分母都为原方程组的系数行列
21 22 11 12 a a a a D = + = + = 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b 2 22 1 12 1 b a b a D = 21 22 11 12 a a a a D = + = + = 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b 12 2 11 1 2 a b a b D = , 21 22 11 12 2 22 1 12 1 1 a a a a b a b a D D x = = 注意: 分母都为原方程组的系数行列式. . 21 22 11 12 21 2 11 1 2 2 a a a a a b a b D D x = = 则该二元线性方程组的解(3)式 11 22 12 21 1 22 12 2 1 a a a a b a a b x − − = 11 22 12 21 11 2 1 21 2 a a a a a b b a x − − = (3) 表示为: