
第二章 矩阵及其运算 习题课 主要内容 x+y= 典型例题 测验题 带助式
转置矩阵 定 特殊矩阵 锡 (反)对称矩阵 方阵行(列)矩阵 幂等矩阵 念 司型矩阵和相等矩阵 对 合矩 阵 矩阵单矩阵 正交矩阵 伴随矩阵 对角矩阵 逆矩阵 定 相关定埋及性质 (下)三角矩阵 矩阵相加 方阵的幂 方阵的行列式 万阵的运算 分块矩阵 运算及具性质 数乘矩阵 矩阵相采 上贝 返回
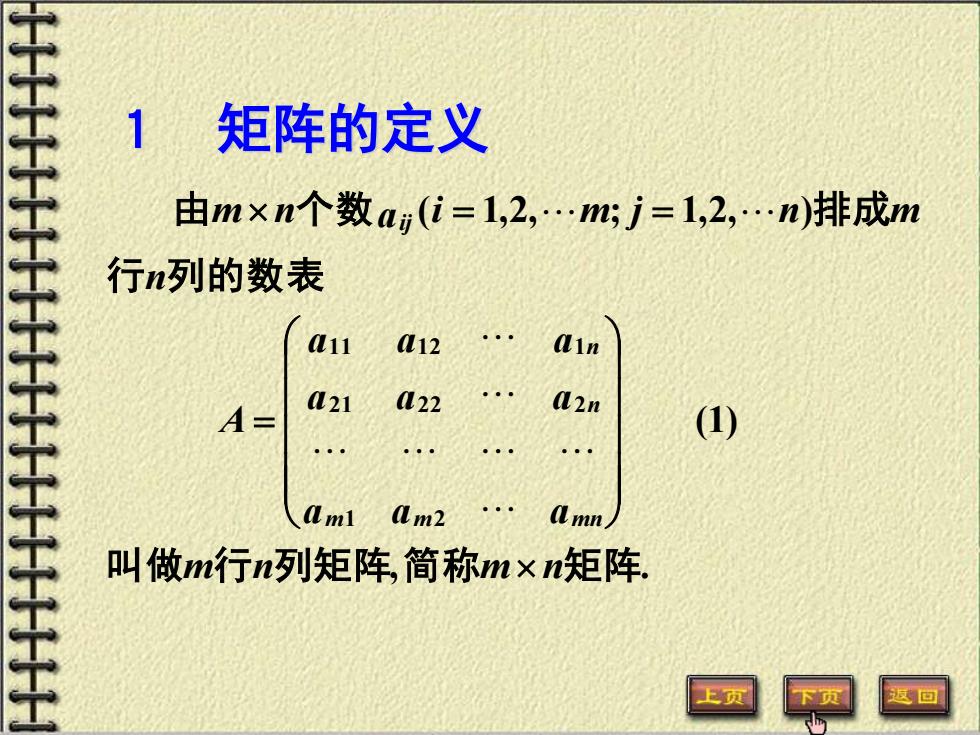
1矩阵的定义 由m×n个数a(i=1,2,.m;j=1,2,.n)排成m 行n列的数表 11 12 Qin A- 021 L22 Q2n (1) Aml am2 amn 叫做m行n列矩阵,简称m×n矩阵. 上页 下页 返回
, . (1) ( 1,2, ; 1,2, ) 1 2 2 1 2 2 2 1 1 1 2 1 叫 做 行 列矩阵 简 称 矩 阵 行 列的数表 由 个 数 排 成 m n m n a a a a a a a a a A n m n a i m j n m m m mn n n ij = = = 1 矩阵的定义

其中m×n个数叫做矩阵A的元素,a:叫做矩 阵A的第行第列元素. 元素是实数的矩阵叫做实矩阵, 元素是复数的矩阵叫做复矩阵 ()式可简记为 A=(ajmxn或A=(a m×n矩阵A也记作Amxm. 上页
. . . , 元素是复数的矩阵叫做复矩阵 元素是实数的矩阵叫做实矩阵 阵 的 第 行 第 列元素 其 中 个数叫做矩阵 的元素 叫做矩 A i j m n A aij . ( ) ( ), (1) m n A A A a A a m n ij m n ij = = 矩 阵 也记作 或 式可简记为

2 方阵! 列矩阵 行矩阵 对(1)式,当m=n时,A称为n阶方阵. 只有一列的矩阵A= 叫做列矩阵 am 只有一行的矩阵A=(a1a2.am)叫做 行矩阵 返回
. ( ) ; 1 2 2 1 行矩阵 只有一行的矩阵 叫 做 只有一列的矩阵 叫做列矩阵 A a a a a a a A n m = = 2 方阵 列矩阵 行矩阵 对(1)式,当m = n时, A称 为n阶方阵